vi.sualize.us user–tag

This is the bipartite picture tagging network of vi.sualize.us. Left nodes represent users and right nodes represent tags. An edge connects a user and a tag he has used.

Metadata

CodeVut
Internal namepics_ut
Namevi.sualize.us user–tag
Data sourcehttp://vi.sualize.us/
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Interaction network
Node meaningUser, tag
Edge meaningAssignment
Network formatBipartite, undirected
Edge typeUnweighted, multiple edges

Statistics

Size n =99,157
Left size n1 =17,122
Right size n2 =82,035
Volume m =2,298,816
Unique edge count m̿ =449,503
Wedge count s =211,070,075
Claw count z =290,844,387,003
Cross count x =596,462,431,865,815
Square count q =519,071,489
4-Tour count T4 =4,997,987,030
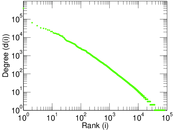
Maximum degree dmax =405,429
Maximum left degree d1max =46,571
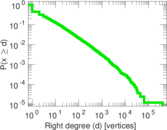
Maximum right degree d2max =405,429
Average degree d =46.367 2
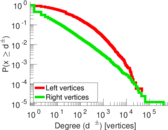
Average left degree d1 =134.261
Average right degree d2 =28.022 4
Fill p =0.000 320 021
Average edge multiplicity m̃ =5.114 13
Size of LCC N =98,486
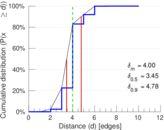
Diameter δ =12
50-Percentile effective diameter δ0.5 =3.453 47
90-Percentile effective diameter δ0.9 =4.781 47
Median distance δM =4
Mean distance δm =4.001 17
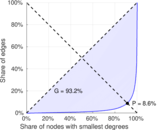
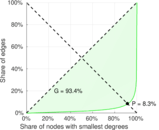
Gini coefficient G =0.940 143
Balanced inequality ratio P =0.082 228 4
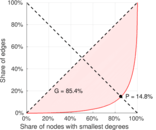
Left balanced inequality ratio P1 =0.148 075
Right balanced inequality ratio P2 =0.083 396 4
Relative edge distribution entropy Her =0.810 950
Power law exponent γ =2.439 72
Tail power law exponent γt =1.701 00
Degree assortativity ρ =−0.106 507
Degree assortativity p-value pρ =0.000 00
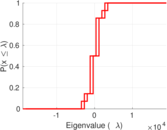
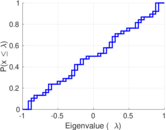
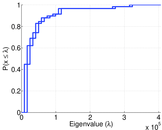
Spectral norm α =18,991.5
Algebraic connectivity a =0.011 268 9
Spectral separation |λ1[A] / λ2[A]| =2.145 22
Controllability C =76,829
Relative controllability Cr =0.774 822

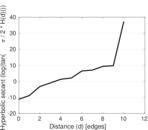
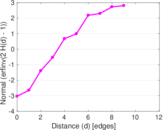
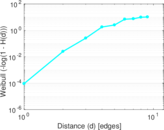
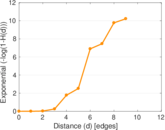
Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Edge weight/multiplicity distribution

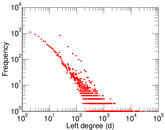
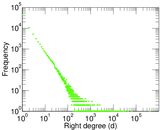
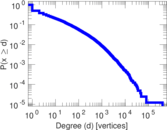
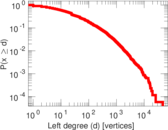
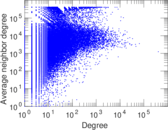
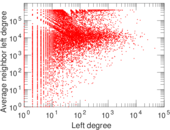
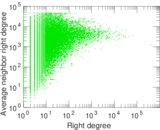
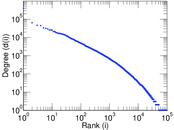
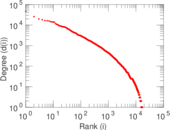
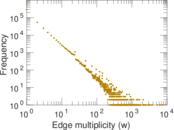
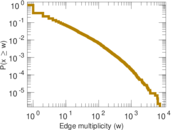
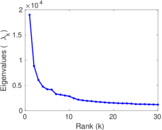
Matrix decompositions plots

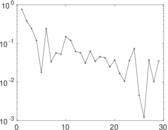
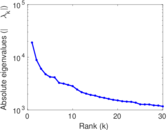
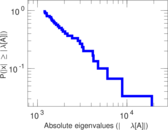
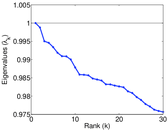
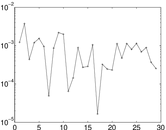
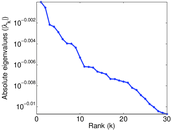
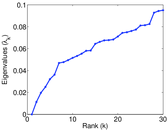
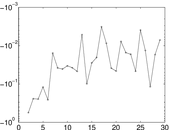
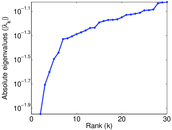
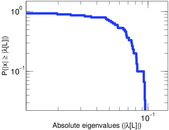
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Nicolas Neubauer and Klaus Obermayer. Analysis of the Visualize.us folksonomy. Unpublished, 2010.