 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee
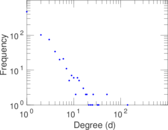
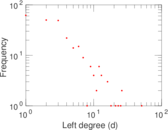
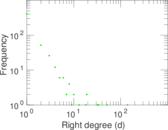
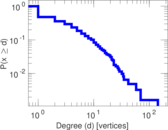
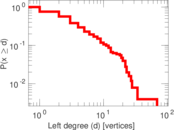
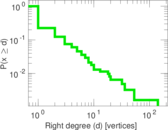
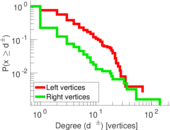
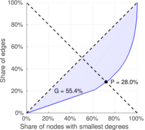
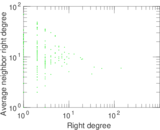
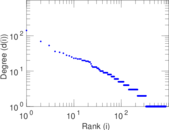
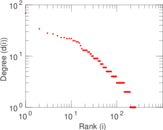
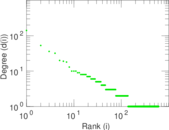
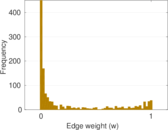
This bipartite network denotes which languages are spoken in which countries. Nodes are countries and languages; edge weights denote the proportion (between zero and one) of the population of a given country speaking a given language. To quote the Unicode data description: "The main goal is to provide approximate figures for the literate, functional population for each language in each territory: that is, the population that is able to read and write each language, and is comfortable enough to use it with computers."
| Code | UL
| |
| Internal name | unicodelang
| |
| Name | Unicode languages | |
| Data source | http://www.unicode.org/cldr/charts/25/supplemental/territory_language_information.html | |
| Availability | Dataset is available for download | |
| Consistency check | Dataset passed all tests | |
| Category | Feature network | |
| Dataset timestamp | 2015 | |
| Node meaning | Country, language | |
| Edge meaning | Hosts | |
| Network format | Bipartite, undirected | |
| Edge type | Positive weights, no multiple edges | |
| Zero weights | Edges may have weight zero |

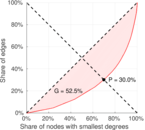
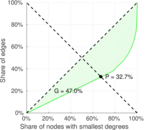
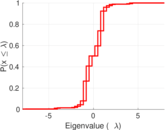
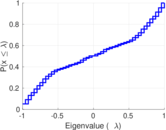
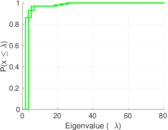


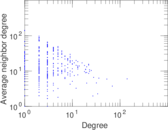
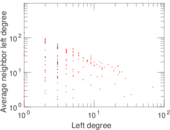
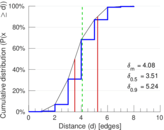
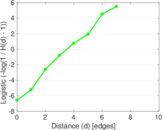
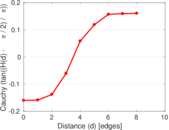
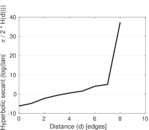
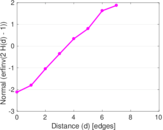
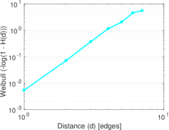
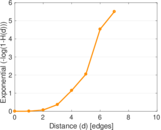




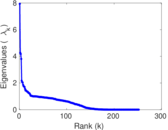
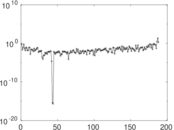
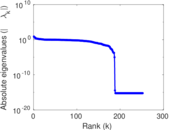
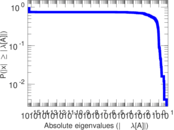
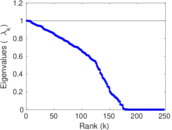
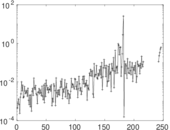
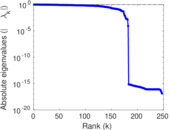
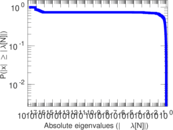
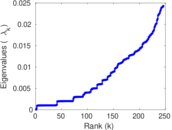
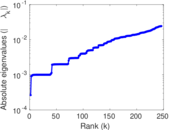
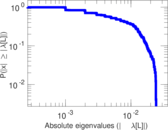
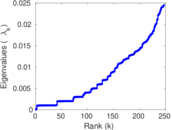

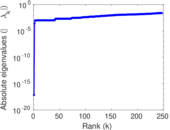
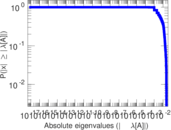
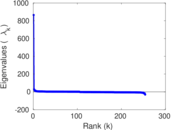
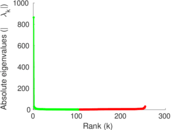
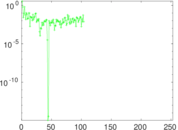
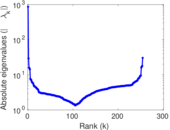
| [1] | Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ] |