Wikipedia categories (en)

This is the bipartite network of English Wikipedia articles and the categories they are contained in. Left nodes are articles and right nodes are categories.

Metadata

Code		`WC`
Internal name		`wiki-en-cat`
Name		Wikipedia categories (en)
Data source		http://dumps.wikimedia.org/
Availability		Dataset is available for download
Consistency check		Dataset passed all tests
Category		Feature network
Node meaning		Article, category
Edge meaning		Inclusion
Network format		Bipartite, undirected
Edge type		Unweighted, no multiple edges

Statistics

Size	n =	2,036,440
Left size	n₁ =	1,853,493
Right size	n₂ =	182,947
Volume	m =	3,795,796
Wedge count	s =	898,164,591
Claw count	z =	1,363,824,377,144
Cross count	x =	3,001,843,059,062,188
Square count	q =	160,976,541
4-Tour count	T₄ =	4,888,065,352
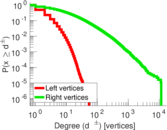
Maximum degree	d_max =	11,593
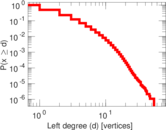
Maximum left degree	d_1max =	54
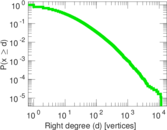
Maximum right degree	d_2max =	11,593
Average degree	d =	3.727 87
Average left degree	d₁ =	2.047 91
Average right degree	d₂ =	20.748 1
Fill	p =	1.119 40 × 10⁻⁵
Size of LCC	N =	1,893,657
Diameter	δ =	46
50-Percentile effective diameter	δ_0.5 =	11.377 1
90-Percentile effective diameter	δ_0.9 =	15.307 2
Median distance	δ_M =	12
Mean distance	δ_m =	11.750 1
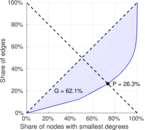
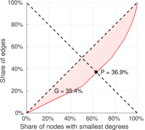
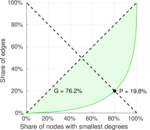
Gini coefficient	G =	0.640 075
Balanced inequality ratio	P =	0.257 484
Left balanced inequality ratio	P₁ =	0.368 946
Right balanced inequality ratio	P₂ =	0.197 671
Relative edge distribution entropy	H_er =	0.902 290
Power law exponent	γ =	2.614 68
Tail power law exponent	γ_t =	2.381 00
Tail power law exponent with p	γ₃ =	2.381 00
p-value	p =	0.000 00
Left tail power law exponent with p	γ_3,1 =	7.071 00
Left p-value	p₁ =	0.435 000
Right tail power law exponent with p	γ_3,2 =	2.261 00
Right p-value	p₂ =	0.000 00
Degree assortativity	ρ =	+0.093 530 5
Degree assortativity p-value	p_ρ =	0.000 00
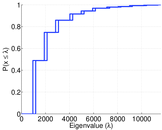
Spectral norm	α =	147.912
Algebraic connectivity	a =	0.000 224 266
Spectral separation	\|λ₁[A] / λ₂[A]\| =	1.095 29
Controllability	C =	1,677,460
Relative controllability	C_r =	0.823 722

Plots

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Delaunay graph drawing

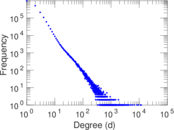
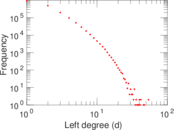
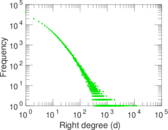
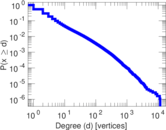
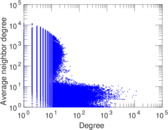
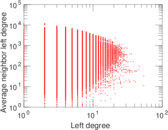
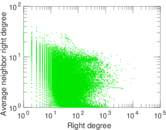
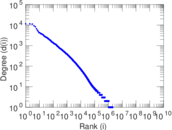
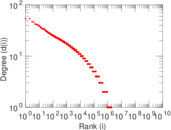
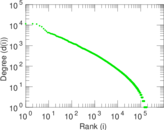
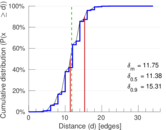
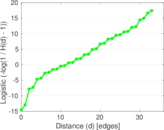
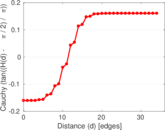
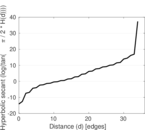
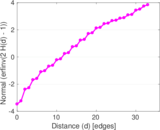
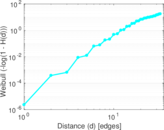
Downloads

Data as TSV (16,386,345 bytes)
Original dataset source

References

[1]	Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2]	Wikimedia Foundation. Wikimedia downloads. http://dumps.wikimedia.org/, January 2010.