arXiv hep-th

This is the co-citation graph of papers of scientific papers from the arXiv's High Energy Physics – Theory (hep-th) section. An edge between two papers represents a paper that cites both papers. Timestamps denote the date of a publication.

Metadata

Code		`TH`
Internal name		`ca-cit-HepTh`
Name		arXiv hep-th
Data source		http://snap.stanford.edu/data/cit-HepTh.html
Availability		Dataset is available for download
Consistency check		Dataset passed all tests
Category		Co-citation network
Node meaning		Author
Edge meaning		Co-citation
Network format		Unipartite, undirected
Edge type		Unweighted, multiple edges
Temporal data		Edges are annotated with timestamps
Loops		Does not contain loops
Join		Is the join of an underlying network

Statistics

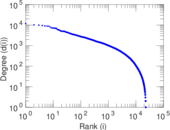
Size	n =	22,908
Volume	m =	2,673,133
Unique edge count	m̿ =	2,444,798
Wedge count	s =	2,134,203,872
Claw count	z =	1,506,168,874,130
Cross count	x =	1,478,988,337,901,334
Triangle count	t =	191,358,360
Square count	q =	92,607,592,200
4-Tour count	T₄ =	749,402,442,684
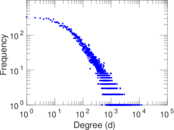
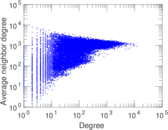
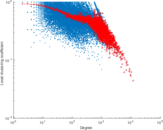
Maximum degree	d_max =	11,967
Average degree	d =	233.380
Fill	p =	0.009 317 89
Average edge multiplicity	m̃ =	1.093 40
Size of LCC	N =	22,721
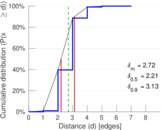
Diameter	δ =	9
50-Percentile effective diameter	δ_0.5 =	2.212 36
90-Percentile effective diameter	δ_0.9 =	3.131 39
Median distance	δ_M =	3
Mean distance	δ_m =	2.717 19
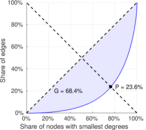
Gini coefficient	G =	0.684 442
Balanced inequality ratio	P =	0.235 728
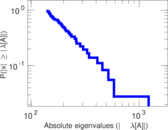
Power law exponent	γ =	1.233 90
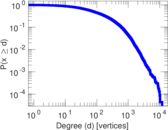
Tail power law exponent	γ_t =	1.721 00
Degree assortativity	ρ =	−0.033 934 3
Degree assortativity p-value	p_ρ =	0.000 00
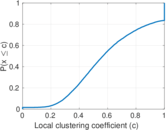
Clustering coefficient	c =	0.268 988
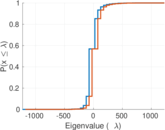
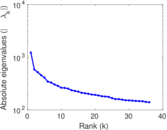
Spectral norm	α =	1,225.32
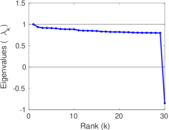
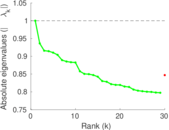
Algebraic connectivity	a =	0.175 383
Spectral separation	\|λ₁[A] / λ₂[A]\| =	2.093 52
Non-bipartivity	b_A =	0.896 403
Normalized non-bipartivity	b_N =	0.152 926
Algebraic non-bipartivity	χ =	0.235 724
Spectral bipartite frustration	b_K =	0.000 273 859
Controllability	C =	22
Relative controllability	C_r =	0.000 960 363

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Edge weight/multiplicity distribution

Clustering coefficient distribution

Average neighbor degree distribution

Temporal distribution

Temporal hop distribution

Diameter/density evolution

SynGraphy

Inter-event distribution

Node-level inter-event distribution

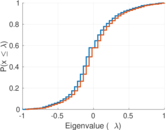
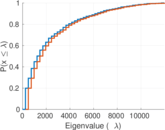
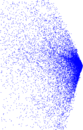
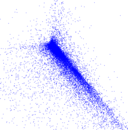
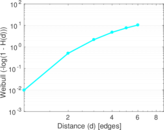
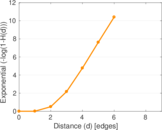
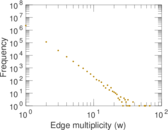
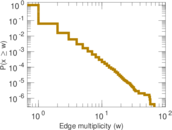
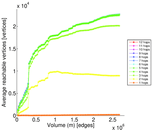
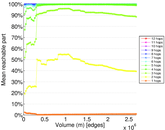
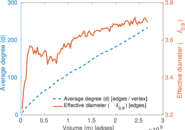
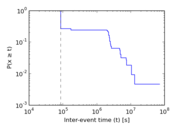
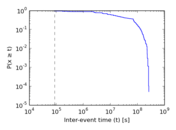
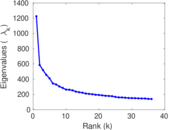
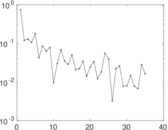
Matrix decompositions plots

Downloads

References

[1]	Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2]	Jure Leskovec, Jon Kleinberg, and Christos Faloutsos. Graph evolution: Densification and shrinking diameters. ACM Trans. Knowl. Discov. from Data, 1(1):1–40, 2007.