Congress votes

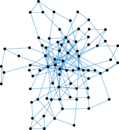
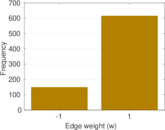
In this network, nodes are politicians speaking in the United States Congress, and a directed edge denotes that a speaker mentions another speaker. The weight of an edge (positive or negative) denotes whether the mention is in support of or opposition to the mentioned politician. Multiple parallel edges are possible. Loops are allowed, i.e., speakers may mention themselves.

Metadata

CodeCO
Internal nameconvote
NameCongress votes
Data sourcehttp://www.cs.cornell.edu/home/llee/data/convote.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Interaction network
Dataset timestamp 2005
Node meaningPolitician
Edge meaningMention
Network formatUnipartite, directed
Edge typeSigned, possibly weighted, multiple edges
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsContains loops

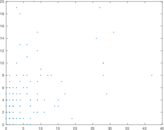
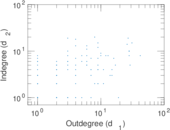
Statistics

Size n =219
Volume m =764
Unique edge count m̿ =587
Loop count l =2
Wedge count s =5,342
Claw count z =45,501
Cross count x =271,364
Triangle count t =212
Square count q =822
4-Tour count T4 =28,986
Maximum degree dmax =50
Maximum outdegree d+max =42
Maximum indegree d−max =20
Average degree d =6.977 17
Fill p =0.012 239 1
Average edge multiplicity m̃ =1.301 53
Size of LCC N =219
Size of LSCC Ns =109
Relative size of LSCC Nrs =0.497 717
Diameter δ =7
50-Percentile effective diameter δ0.5 =2.670 51
90-Percentile effective diameter δ0.9 =3.870 71
Median distance δM =3
Mean distance δm =3.183 69
Gini coefficient G =0.533 064
Balanced inequality ratio P =0.290 460
Outdegree balanced inequality ratio P+ =0.287 905
Indegree balanced inequality ratio P− =0.337 308
Relative edge distribution entropy Her =0.906 903
Power law exponent γ =1.927 99
Tail power law exponent γt =3.191 00
Tail power law exponent with p γ3 =3.191 00
p-value p =0.620 000
Outdegree tail power law exponent with p γ3,o =2.931 00
Outdegree p-value po =0.108 000
Indegree tail power law exponent with p γ3,i =3.151 00
Indegree p-value pi =0.129 000
Degree assortativity ρ =−0.339 502
Degree assortativity p-value pρ =1.596 11 × 10−29
In/outdegree correlation ρ± =+0.472 475
Clustering coefficient c =0.119 057
Directed clustering coefficient c± =0.101 391
Spectral norm α =17.836 0
Operator 2-norm ν =11.830 7
Cyclic eigenvalue π =7.185 98
Algebraic connectivity a =0.492 405
Spectral separation |λ1[A] / λ2[A]| =1.116 10
Reciprocity y =0.221 465
Non-bipartivity bA =0.332 336
Normalized non-bipartivity bN =0.237 671
Algebraic non-bipartivity χ =0.358 762
Spectral bipartite frustration bK =0.018 778 4
Negativity ζ =0.195 911
Algebraic conflict ξ =0.166 891
Triadic conflict τ =0.033 018 9
Spectral signed frustration φ =0.008 768 99
Controllability C =119
Relative controllability Cr =0.543 379

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

In/outdegree scatter plot

Item rating evolution

Edge weight/multiplicity distribution

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

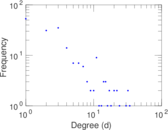
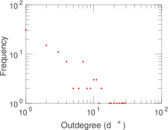
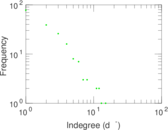
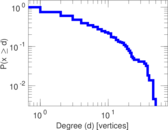
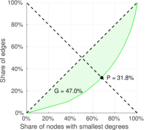
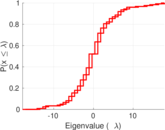
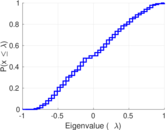
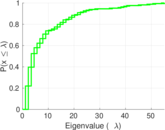
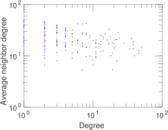
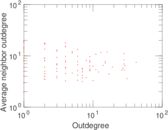
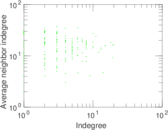
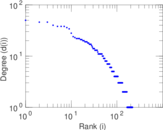
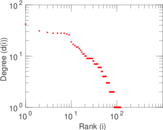
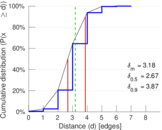
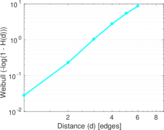
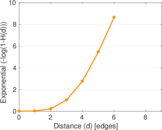
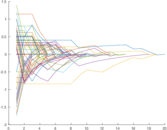
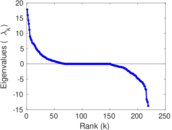
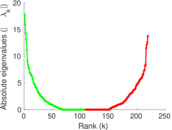
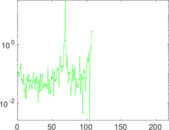
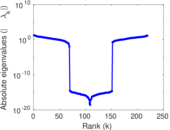
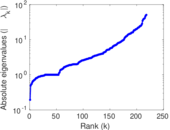
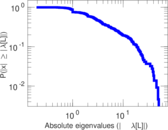
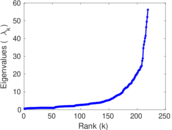
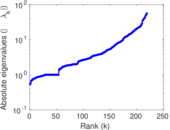
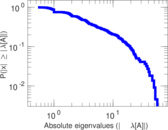
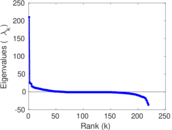
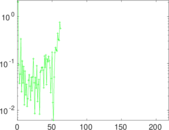
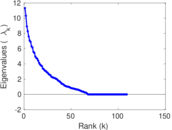
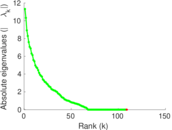
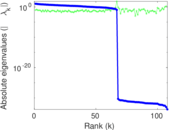
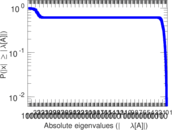
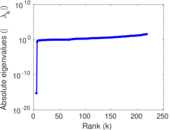
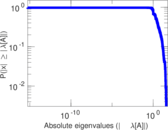
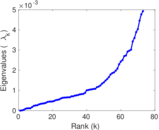
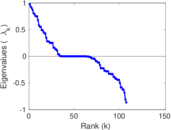
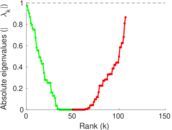
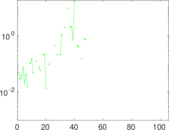
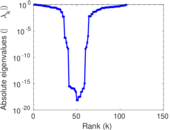
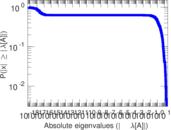
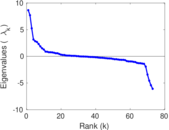
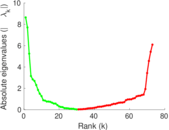
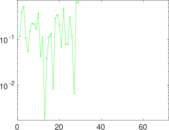
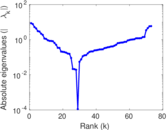
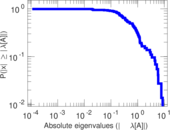
Matrix decompositions plots

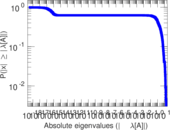
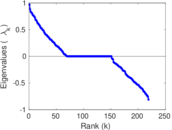
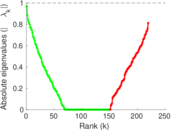
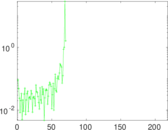
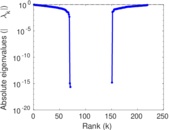
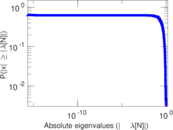
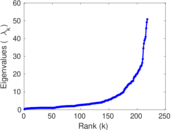
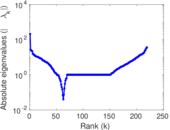
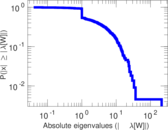
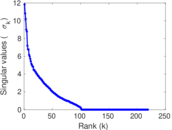
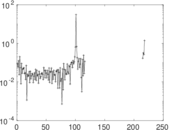
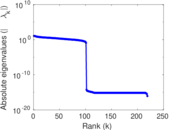
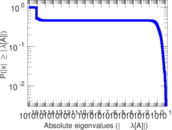
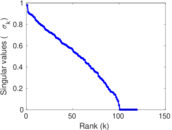
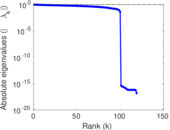
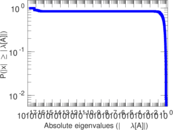
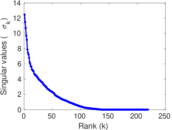
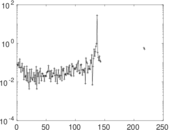
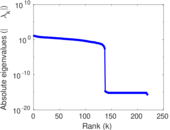
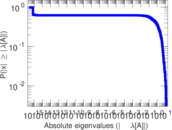
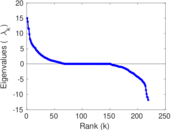
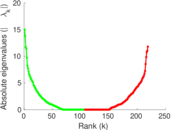
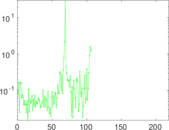
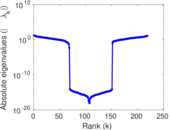
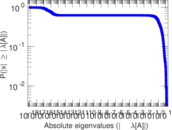
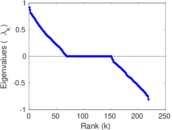
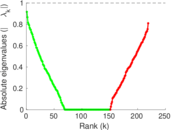
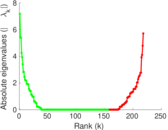
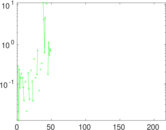
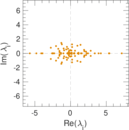
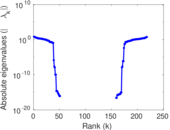
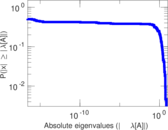
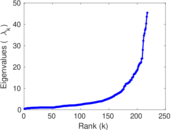
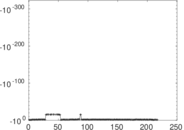
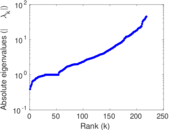
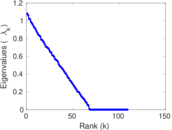
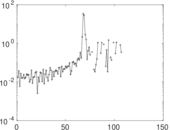
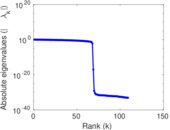
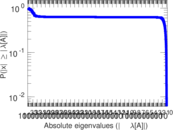
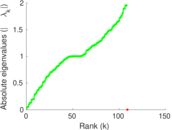
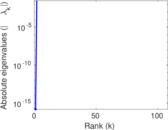
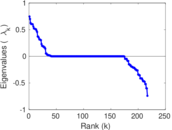
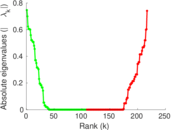
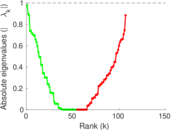
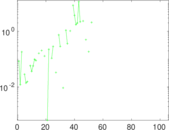
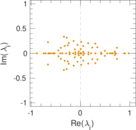
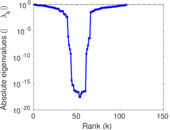
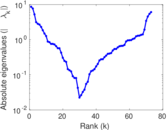
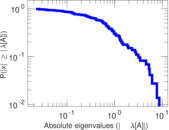
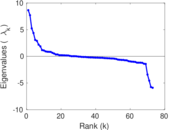
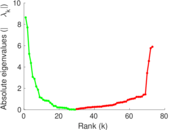
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Matt Thomas, Bo Pang, and Lillian Lee. Get the out vote: Determining support or opposition from congressional floor-debate transcripts. In Proc. Conf. on Empir. Methods in Nat. Lang. Process., pages 327–335, 2006.