DBLP
This is the citation network of DBLP, a database of scientific publications
such as papers and books. Each node in the network is a publication, and each
edge represents a citation of a publication by another publication. In other
words, the directed edge (A → B) denotes that publication A cites publication
B. Publications are allowed to cite themselves, and therefore the network
contains loops. The original dataset contains a small number (<100) of
erroneous duplicate edges, i.e., a paper citing another paper multiple times.
These have been removed from this version of the dataset.
Metadata
Statistics
| Size | n = | 12,590
|
| Volume | m = | 49,759
|
| Loop count | l = | 15
|
| Wedge count | s = | 2,124,720
|
| Claw count | z = | 172,872,369
|
| Cross count | x = | 22,368,563,858
|
| Triangle count | t = | 43,896
|
| Square count | q = | 787,154
|
| 4-Tour count | T4 = | 14,895,384
|
| Maximum degree | dmax = | 714
|
| Maximum outdegree | d+max = | 617
|
| Maximum indegree | d−max = | 227
|
| Average degree | d = | 7.904 53
|
| Fill | p = | 0.000 313 921
|
| Size of LCC | N = | 12,494
|
| Size of LSCC | Ns = | 240
|
| Relative size of LSCC | Nrs = | 0.019 062 7
|
| Diameter | δ = | 10
|
| 50-Percentile effective diameter | δ0.5 = | 3.847 50
|
| 90-Percentile effective diameter | δ0.9 = | 4.997 88
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 4.372 20
|
| Gini coefficient | G = | 0.657 631
|
| Balanced inequality ratio | P = | 0.234 611
|
| Outdegree balanced inequality ratio | P+ = | 0.361 683
|
| Indegree balanced inequality ratio | P− = | 0.262 244
|
| Relative edge distribution entropy | Her = | 0.907 783
|
| Power law exponent | γ = | 1.837 27
|
| Tail power law exponent | γt = | 3.391 00
|
| Tail power law exponent with p | γ3 = | 3.391 00
|
| p-value | p = | 0.466 000
|
| Outdegree tail power law exponent with p | γ3,o = | 3.611 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 2.711 00
|
| Indegree p-value | pi = | 0.054 000 0
|
| Degree assortativity | ρ = | −0.045 724 6
|
| Degree assortativity p-value | pρ = | 4.224 43 × 10−47
|
| In/outdegree correlation | ρ± = | +0.011 711 9
|
| Clustering coefficient | c = | 0.061 979 0
|
| Directed clustering coefficient | c± = | 0.096 706 4
|
| Spectral norm | α = | 43.054 6
|
| Operator 2-norm | ν = | 34.102 3
|
| Cyclic eigenvalue | π = | 4.676 83
|
| Algebraic connectivity | a = | 0.085 199 2
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.390 85
|
| Reciprocity | y = | 0.004 642 38
|
| Non-bipartivity | bA = | 0.331 103
|
| Normalized non-bipartivity | bN = | 0.047 487 4
|
| Algebraic non-bipartivity | χ = | 0.085 170 6
|
| Spectral bipartite frustration | bK = | 0.002 682 08
|
| Controllability | C = | 9,453
|
| Relative controllability | Cr = | 0.750 834
|
Plots

















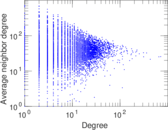

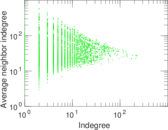




























Matrix decompositions plots













































































































Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Michael Ley.
The DBLP computer science bibliography: Evolution, research issues,
perspectives.
In Proc. Int. Symposium on String Process. and Inf. Retr.,
pages 1–10, 2002.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee




























































































































































