Digg friends

This is the directed friendship graph of Digg, collected in 2009.

Metadata

CodeDF
Internal namedigg-friends
NameDigg friends
Data sourcehttp://www.isi.edu/~lerman/downloads/digg2009.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Online social network
Dataset timestamp 2009
Node meaningUser
Edge meaningVote
Network formatUnipartite, directed
Edge typeUnweighted, no multiple edges
Temporal data Edges are annotated with timestamps
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsDoes not contain loops
Snapshot Is a snapshot and likely to not contain all data

Statistics

Size n =279,630
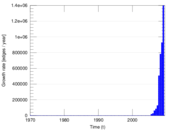
Volume m =1,731,653
Wedge count s =695,297,099
Claw count z =797,470,104,176
Cross count x =1,546,289,679,690,330
Triangle count t =14,236,438
Square count q =4,925,314,153
4-Tour count T4 =42,186,797,872
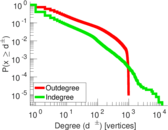
Maximum degree dmax =12,204
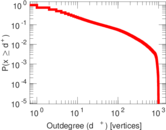
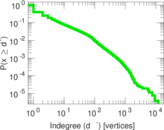
Maximum outdegree d+max =995
Maximum indegree d−max =12,038
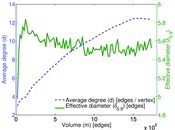
Average degree d =12.385 3
Fill p =2.214 60 × 10−5
Size of LCC N =261,489
Diameter δ =18
50-Percentile effective diameter δ0.5 =3.719 89
90-Percentile effective diameter δ0.9 =4.962 37
Median distance δM =4
Mean distance δm =4.307 22
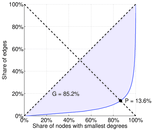
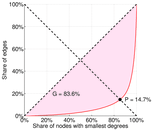
Gini coefficient G =0.852 351
Balanced inequality ratio P =0.136 055
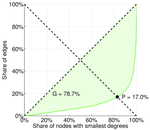
Outdegree balanced inequality ratio P+ =0.146 953
Indegree balanced inequality ratio P− =0.170 457
Power law exponent γ =2.225 48
Tail power law exponent γt =1.751 00
Degree assortativity ρ =−0.055 709 6
Degree assortativity p-value pρ =0.000 00
In/outdegree correlation ρ± =+0.369 215
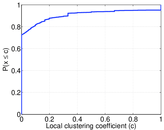
Clustering coefficient c =0.061 426 0
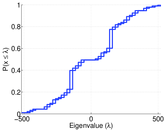
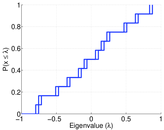
Spectral norm α =518.890
Operator 2-norm ν =348.560
Cyclic eigenvalue π =170.320
Algebraic connectivity a =0.003 957 60
Reciprocity y =0.211 967
Non-bipartivity bA =0.602 264
Normalized non-bipartivity bN =0.005 757 20
Algebraic non-bipartivity χ =0.011 289 4
Spectral bipartite frustration bK =0.000 240 148
Controllability C =215,907
Relative controllability Cr =0.772 117

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Delaunay graph drawing

In/outdegree scatter plot

Clustering coefficient distribution

Temporal distribution

Diameter/density evolution

SynGraphy

Inter-event distribution

Node-level inter-event distribution

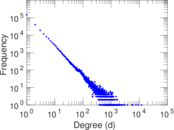
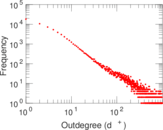
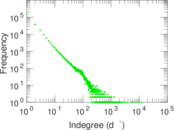
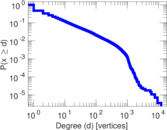
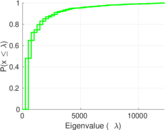
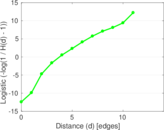
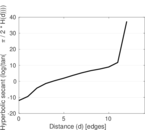
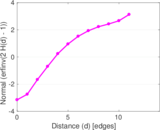
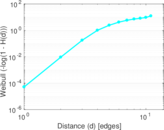
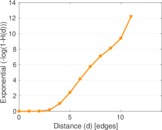
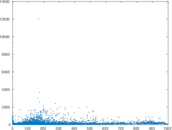
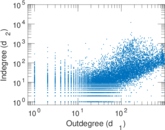
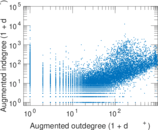
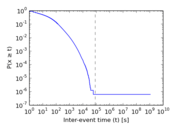
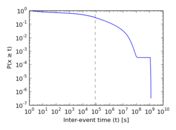
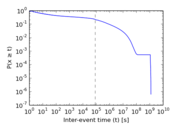
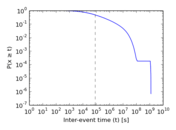
Matrix decompositions plots

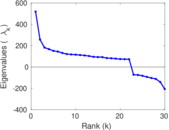
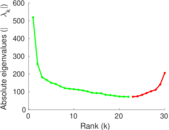
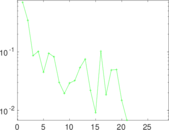
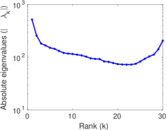
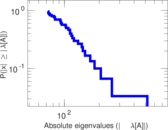
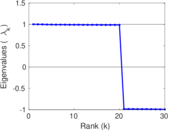
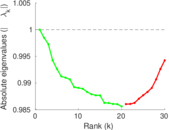
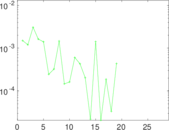
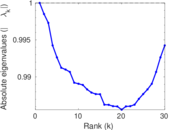
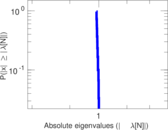
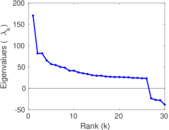
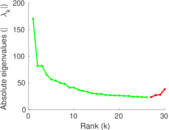
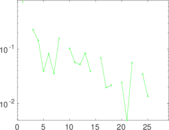
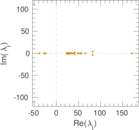
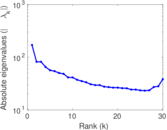
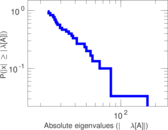
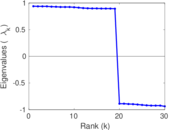
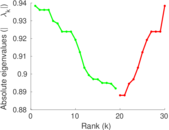
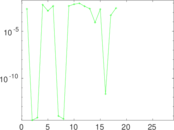
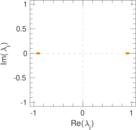
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] T. Hogg and K. Lerman. Social dynamics of Digg. Eur. Phys. J. Data Sci., 1(5), 2012.