DNC emails
This is the directed network of emails in the 2016 Democratic National
Committee email leak. The Democratic National Committee (DNC) is the formal
governing body for the United States Democratic Party. A dump of emails of the
DNC was leaked in 2016. Nodes in the network correspond to persons in the
dataset. A directed edge in the dataset denotes that a person has sent an
email to another person. Since an email can have any number of recipients, a
single email is mapped to multiple edges in this dataset, resulting in the
number of edges in this network being about twice the number of emails in the
dump.
Metadata
Statistics
| Size | n = | 2,029
|
| Volume | m = | 39,264
|
| Unique edge count | m̿ = | 5,598
|
| Wedge count | s = | 317,905
|
| Claw count | z = | 59,899,010
|
| Cross count | x = | 6,944,032,926
|
| Triangle count | t = | 9,431
|
| Square count | q = | 209,206
|
| 4-Tour count | T4 = | 2,954,036
|
| Maximum degree | dmax = | 5,813
|
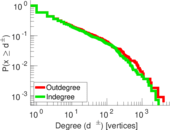
| Maximum outdegree | d+max = | 4,073
|
| Maximum indegree | d−max = | 2,951
|
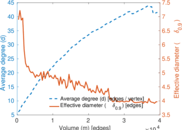
| Average degree | d = | 38.702 8
|
| Fill | p = | 0.001 565 49
|
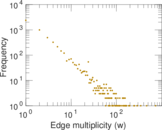
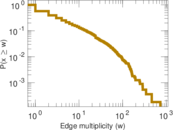
| Average edge multiplicity | m̃ = | 7.013 93
|
| Size of LCC | N = | 1,833
|
| Size of LSCC | Ns = | 520
|
| Relative size of LSCC | Nrs = | 0.256 284
|
| Diameter | δ = | 8
|
| 50-Percentile effective diameter | δ0.5 = | 2.824 58
|
| 90-Percentile effective diameter | δ0.9 = | 3.982 21
|
| Median distance | δM = | 3
|
| Mean distance | δm = | 3.378 96
|
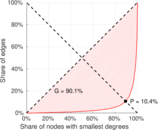
| Gini coefficient | G = | 0.911 291
|
| Balanced inequality ratio | P = | 0.096 653 4
|
| Outdegree balanced inequality ratio | P+ = | 0.104 498
|
| Indegree balanced inequality ratio | P− = | 0.112 419
|
| Relative edge distribution entropy | Her = | 0.790 349
|
| Power law exponent | γ = | 2.773 64
|
| Tail power law exponent | γt = | 2.011 00
|
| Tail power law exponent with p | γ3 = | 2.011 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 1.951 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 2.011 00
|
| Indegree p-value | pi = | 0.004 000 00
|
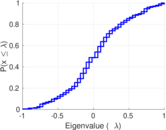
| Degree assortativity | ρ = | −0.306 550
|
| Degree assortativity p-value | pρ = | 3.924 42 × 10−190
|
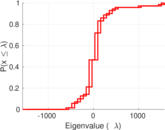
| Spectral norm | α = | 1,566.51
|
| Algebraic connectivity | a = | 0.047 944 7
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.073 48
|
| Reciprocity | y = | 0.419 257
|
| Controllability | C = | 1,500
|
| Relative controllability | Cr = | 0.793 231
|
Plots




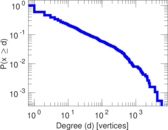
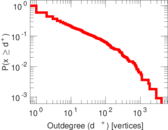
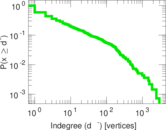







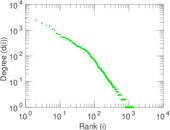
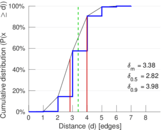




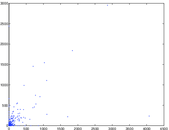
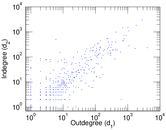
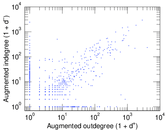






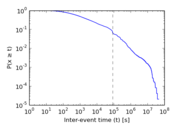
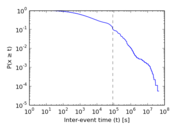
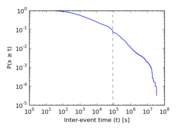
Matrix decompositions plots




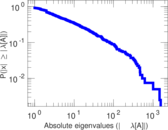




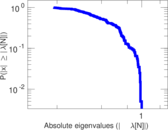



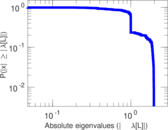



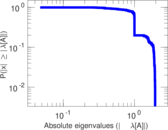
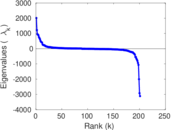


Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee