Wikipedia edits (mi)

This is the bipartite edit network of the Maori Wikipedia. It contains users and pages from the Maori Wikipedia, connected by edit events. Each edge represents an edit. The dataset includes the timestamp of each edit.

Metadata

Codemi
Internal nameedit-miwiki
NameWikipedia edits (mi)
Data sourcehttp://dumps.wikimedia.org/
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Authorship network
Dataset timestamp 2017-10-20
Node meaningUser, article
Edge meaningEdit
Network formatBipartite, undirected
Edge typeUnweighted, multiple edges
Temporal data Edges are annotated with timestamps

Statistics

Size n =13,743
Left size n1 =1,041
Right size n2 =12,702
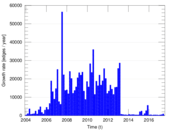
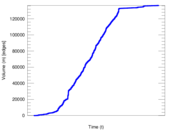
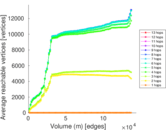
Volume m =136,602
Unique edge count m̿ =60,346
Wedge count s =54,978,210
Claw count z =58,478,700,298
Cross count x =60,567,473,013,521
Square count q =151,424,773
4-Tour count T4 =1,431,451,712
Maximum degree dmax =15,318
Maximum left degree d1max =15,318
Maximum right degree d2max =409
Average degree d =19.879 5
Average left degree d1 =131.222
Average right degree d2 =10.754 4
Fill p =0.004 563 79
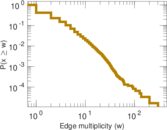
Average edge multiplicity m̃ =2.263 65
Size of LCC N =13,086
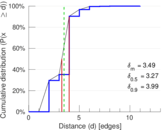
Diameter δ =13
50-Percentile effective diameter δ0.5 =3.267 37
90-Percentile effective diameter δ0.9 =3.992 87
Median distance δM =4
Mean distance δm =3.486 48
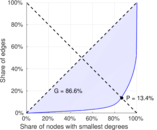
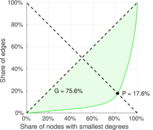
Gini coefficient G =0.865 569
Balanced inequality ratio P =0.144 668
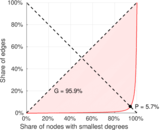
Left balanced inequality ratio P1 =0.057 180 7
Right balanced inequality ratio P2 =0.176 059
Relative edge distribution entropy Her =0.741 807
Power law exponent γ =2.331 81
Tail power law exponent γt =1.831 00
Tail power law exponent with p γ3 =1.831 00
p-value p =0.000 00
Left tail power law exponent with p γ3,1 =1.481 00
Left p-value p1 =0.001 000 00
Right tail power law exponent with p γ3,2 =5.291 00
Right p-value p2 =0.002 000 00
Degree assortativity ρ =−0.404 662
Degree assortativity p-value pρ =0.000 00
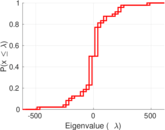
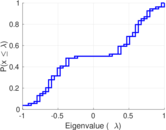
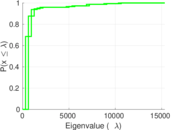
Spectral norm α =615.219
Algebraic connectivity a =0.025 537 6
Spectral separation |λ1[A] / λ2[A]| =1.314 73
Controllability C =11,763
Relative controllability Cr =0.861 569

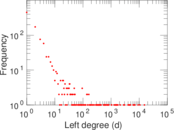
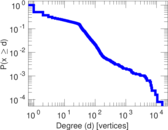
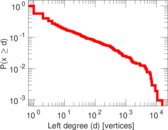
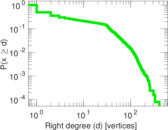
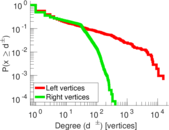
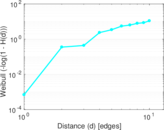
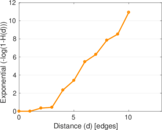
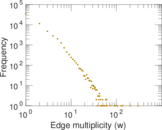
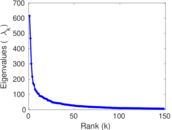
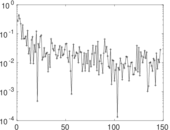
Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Edge weight/multiplicity distribution

Temporal distribution

Temporal hop distribution

Diameter/density evolution

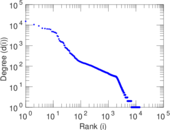
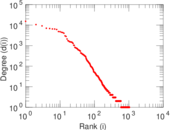
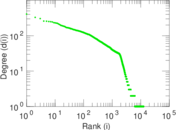
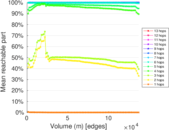
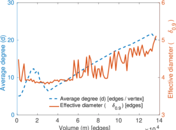
Matrix decompositions plots

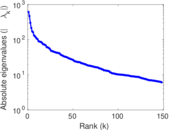
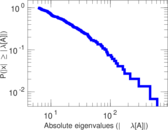
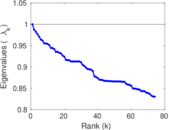
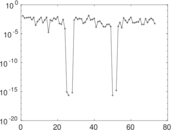
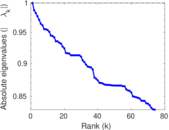
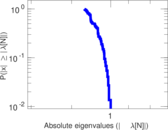
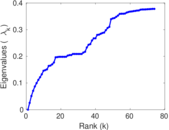
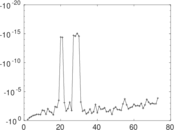
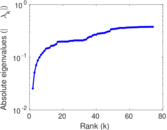
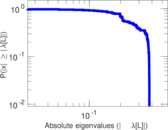
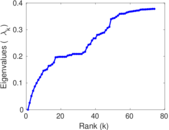
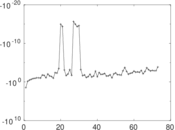
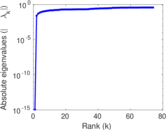
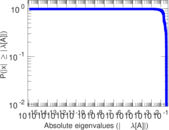
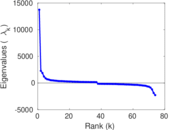
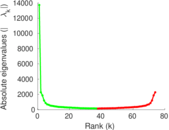
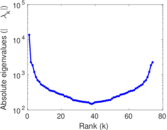
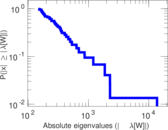
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Wikimedia Foundation. Wikimedia downloads. http://dumps.wikimedia.org/, January 2010.