Wiktionary edits (sv)

This is the bipartite edit network of the Swedish Wiktionary. It contains users and pages from the Swedish Wiktionary, connected by edit events. Each edge represents an edit. The dataset includes the timestamp of each edit.

Metadata

Codemsv
Internal nameedit-svwiktionary
NameWiktionary edits (sv)
Data sourcehttp://dumps.wikimedia.org/
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Authorship network
Dataset timestamp 2017-10-20
Node meaningUser, article
Edge meaningEdit
Network formatBipartite, undirected
Edge typeUnweighted, multiple edges
Temporal data Edges are annotated with timestamps

Statistics

Size n =624,325
Left size n1 =2,340
Right size n2 =621,985
Volume m =2,728,074
Unique edge count m̿ =1,712,445
Wedge count s =121,806,057,857
Claw count z =11,082,853,059,264,392
Cross count x =8.563 01 × 1020
Square count q =42,604,063,037
4-Tour count T4 =828,060,985,674
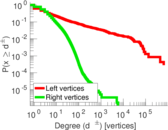
Maximum degree dmax =650,950
Maximum left degree d1max =650,950
Maximum right degree d2max =5,800
Average degree d =8.739 28
Average left degree d1 =1,165.84
Average right degree d2 =4.386 08
Fill p =0.001 176 58
Average edge multiplicity m̃ =1.593 09
Size of LCC N =572,945
Diameter δ =13
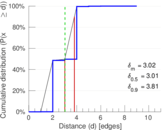
50-Percentile effective diameter δ0.5 =3.005 95
90-Percentile effective diameter δ0.9 =3.808 31
Median distance δM =4
Mean distance δm =3.022 11
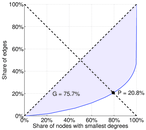
Gini coefficient G =0.757 736
Balanced inequality ratio P =0.207 172
Left balanced inequality ratio P1 =0.021 320 2
Right balanced inequality ratio P2 =0.308 481
Power law exponent γ =2.228 47
Tail power law exponent γt =2.961 00
Tail power law exponent with p γ3 =2.961 00
p-value p =0.000 00
Left tail power law exponent with p γ3,1 =1.451 00
Left p-value p1 =0.015 000 0
Right tail power law exponent with p γ3,2 =5.131 00
Right p-value p2 =0.000 00
Degree assortativity ρ =−0.301 992
Degree assortativity p-value pρ =0.000 00
Spectral norm α =4,465.17
Algebraic connectivity a =0.043 365 1
Spectral separation |λ1[A] / λ2[A]| =2.284 46
Controllability C =568,934
Relative controllability Cr =0.992 277

Plots

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Delaunay graph drawing

Edge weight/multiplicity distribution

Temporal distribution

Diameter/density evolution

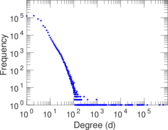
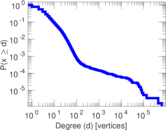
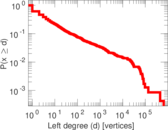
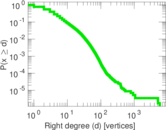
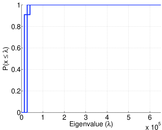
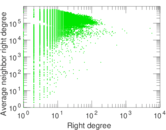
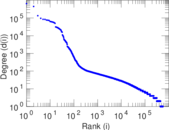
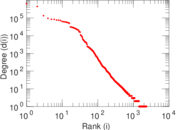
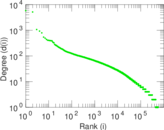
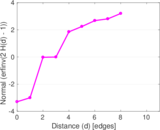
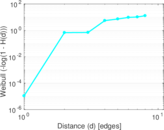
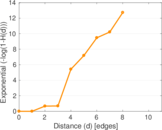
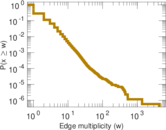
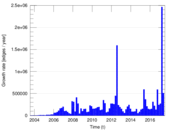
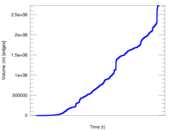
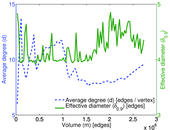
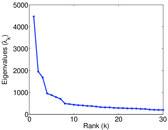
Matrix decompositions plots

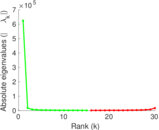
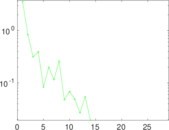
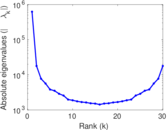
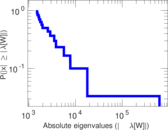
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Wikimedia Foundation. Wikimedia downloads. http://dumps.wikimedia.org/, January 2010.