Wiktionary edits (wa)

This is the bipartite edit network of the Walloon Wiktionary. It contains users and pages from the Walloon Wiktionary, connected by edit events. Each edge represents an edit. The dataset includes the timestamp of each edit.

Metadata

Codemwa
Internal nameedit-wawiktionary
NameWiktionary edits (wa)
Data sourcehttp://dumps.wikimedia.org/
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Authorship network
Dataset timestamp 2017-10-20
Node meaningUser, article
Edge meaningEdit
Network formatBipartite, undirected
Edge typeUnweighted, multiple edges
Temporal data Edges are annotated with timestamps

Statistics

Size n =46,386
Left size n1 =310
Right size n2 =46,076
Volume m =182,251
Unique edge count m̿ =100,917
Wedge count s =771,842,591
Claw count z =5,979,787,692,180
Cross count x =37,679,772,457,299,112
Square count q =159,503,737
4-Tour count T4 =4,363,602,390
Maximum degree dmax =82,442
Maximum left degree d1max =82,442
Maximum right degree d2max =836
Average degree d =7.858 02
Average left degree d1 =587.906
Average right degree d2 =3.955 44
Fill p =0.007 065 26
Average edge multiplicity m̃ =1.805 95
Size of LCC N =46,058
Diameter δ =15
50-Percentile effective diameter δ0.5 =1.932 25
90-Percentile effective diameter δ0.9 =3.822 25
Median distance δM =2
Mean distance δm =2.964 66
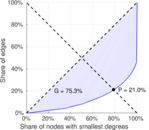
Gini coefficient G =0.752 993
Balanced inequality ratio P =0.209 623
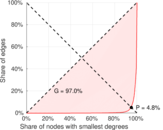
Left balanced inequality ratio P1 =0.047 846 1
Right balanced inequality ratio P2 =0.307 093
Relative edge distribution entropy Her =0.669 572
Power law exponent γ =2.745 94
Tail power law exponent γt =3.861 00
Tail power law exponent with p γ3 =3.861 00
p-value p =0.000 00
Left tail power law exponent with p γ3,1 =1.421 00
Left p-value p1 =0.046 000 0
Right tail power law exponent with p γ3,2 =4.161 00
Right p-value p2 =0.000 00
Degree assortativity ρ =−0.440 211
Degree assortativity p-value pρ =0.000 00
Spectral norm α =1,234.89
Algebraic connectivity a =0.008 811 63
Spectral separation |λ1[A] / λ2[A]| =2.286 81
Controllability C =45,699
Relative controllability Cr =0.987 382

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Edge weight/multiplicity distribution

Temporal distribution

Temporal hop distribution

Diameter/density evolution

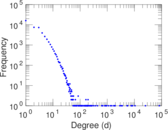
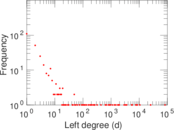
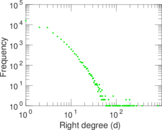
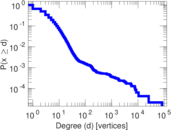
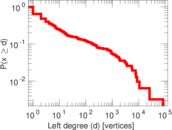
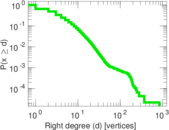
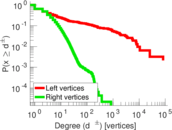
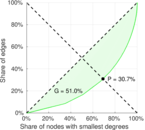
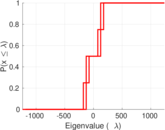
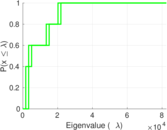
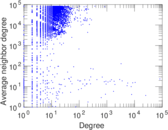
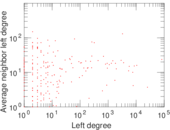
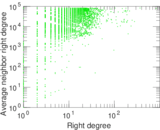
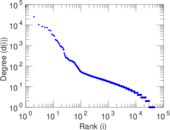
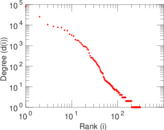
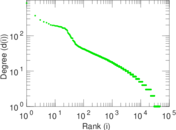
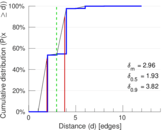
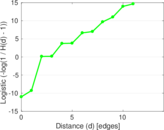
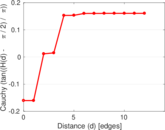
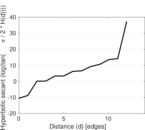
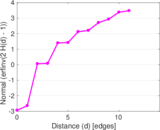
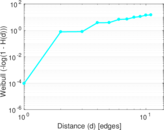
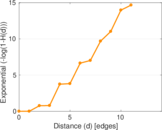
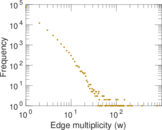
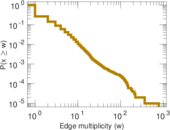
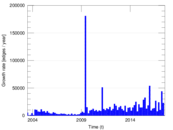
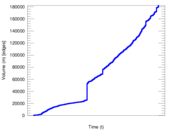
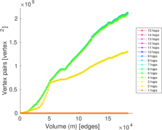
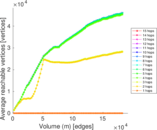
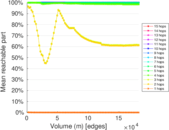
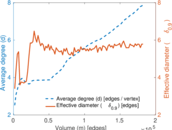
Matrix decompositions plots

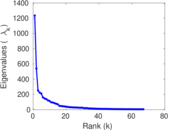
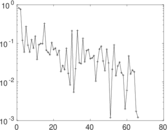
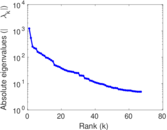
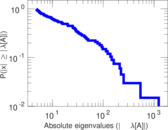
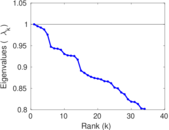
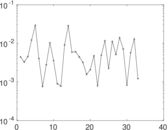
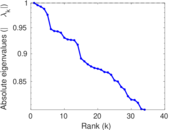
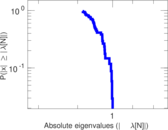
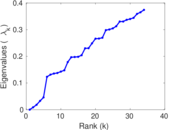
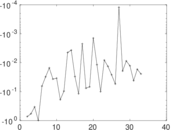
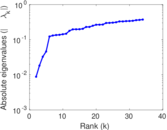
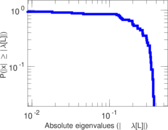
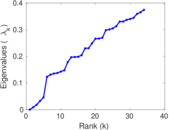
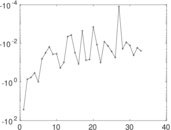
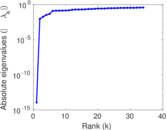
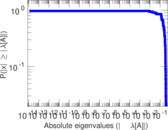
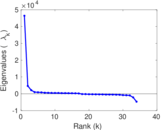
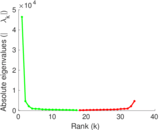
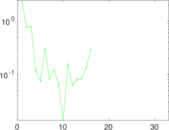
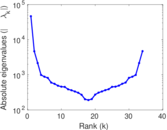
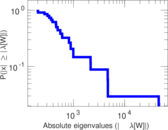
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Wikimedia Foundation. Wikimedia downloads. http://dumps.wikimedia.org/, January 2010.