Wiktionary edits (zu)
This is the bipartite edit network of the Zulu Wiktionary. It contains users
and pages from the Zulu Wiktionary, connected by edit events. Each edge
represents an edit. The dataset includes the timestamp of each edit.
Metadata
Statistics
| Size | n = | 1,624
|
| Left size | n1 = | 214
|
| Right size | n2 = | 1,410
|
| Volume | m = | 7,532
|
| Unique edge count | m̿ = | 4,175
|
| Wedge count | s = | 566,744
|
| Claw count | z = | 73,191,615
|
| Cross count | x = | 8,209,828,076
|
| Square count | q = | 536,179
|
| 4-Tour count | T4 = | 6,565,066
|
| Maximum degree | dmax = | 1,898
|
| Maximum left degree | d1max = | 1,898
|
| Maximum right degree | d2max = | 45
|
| Average degree | d = | 9.275 86
|
| Average left degree | d1 = | 35.196 3
|
| Average right degree | d2 = | 5.341 84
|
| Fill | p = | 0.013 836 4
|
| Average edge multiplicity | m̃ = | 1.804 07
|
| Size of LCC | N = | 1,297
|
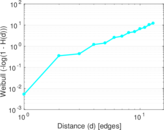
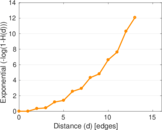
| Diameter | δ = | 14
|
| 50-Percentile effective diameter | δ0.5 = | 3.428 97
|
| 90-Percentile effective diameter | δ0.9 = | 5.863 69
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 4.048 21
|
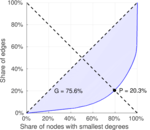
| Gini coefficient | G = | 0.744 127
|
| Balanced inequality ratio | P = | 0.214 485
|
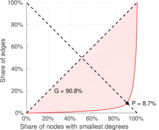
| Left balanced inequality ratio | P1 = | 0.086 564 0
|
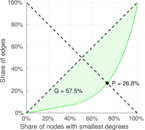
| Right balanced inequality ratio | P2 = | 0.268 322
|
| Relative edge distribution entropy | Her = | 0.787 024
|
| Power law exponent | γ = | 2.290 85
|
| Tail power law exponent | γt = | 1.811 00
|
| Tail power law exponent with p | γ3 = | 1.811 00
|
| p-value | p = | 0.000 00
|
| Left tail power law exponent with p | γ3,1 = | 1.681 00
|
| Left p-value | p1 = | 0.144 000
|
| Right tail power law exponent with p | γ3,2 = | 8.991 00
|
| Right p-value | p2 = | 0.687 000
|
| Degree assortativity | ρ = | +0.097 374 1
|
| Degree assortativity p-value | pρ = | 2.884 59 × 10−10
|
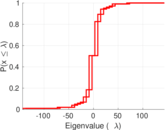
| Spectral norm | α = | 143.618
|
| Algebraic connectivity | a = | 0.016 940 8
|
| Spectral separation | |λ1[A] / λ2[A]| = | 2.115 06
|
| Controllability | C = | 1,200
|
| Relative controllability | Cr = | 0.741 656
|
Plots

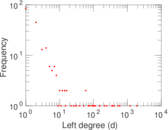

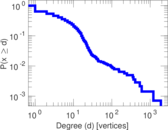
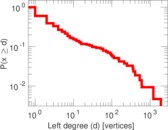
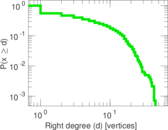
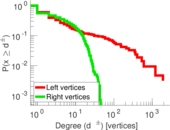
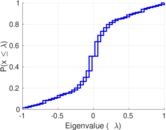



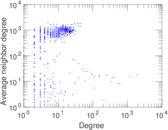

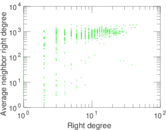
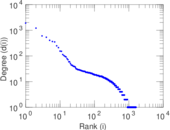
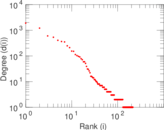
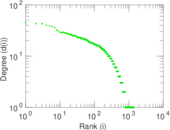
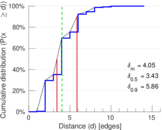



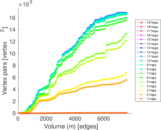
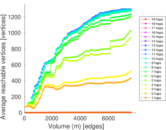
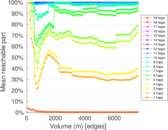
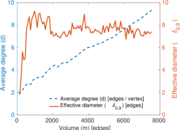
Matrix decompositions plots
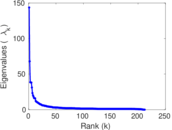
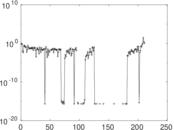
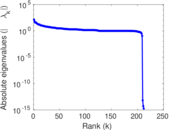
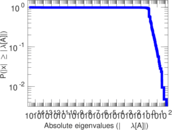
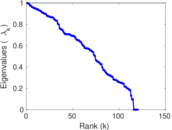
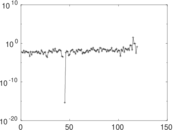
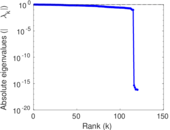
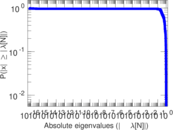
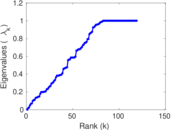
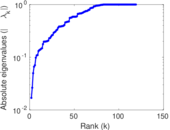
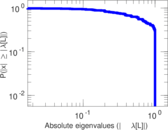
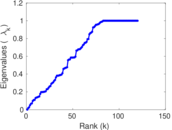
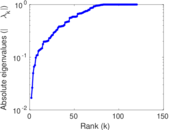
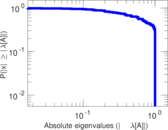
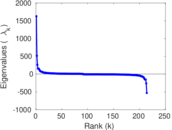
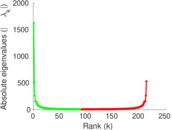
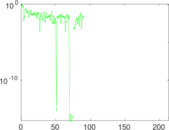
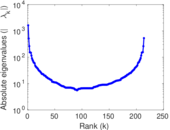
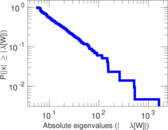
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Wikimedia Foundation.
Wikimedia downloads.
http://dumps.wikimedia.org/, January 2010.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee