Ligue 1 (2016/2017)

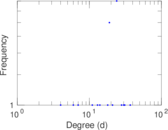
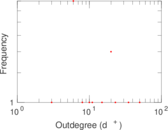
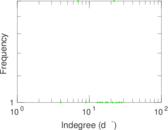
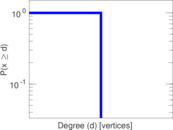
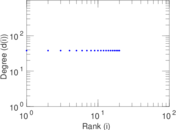
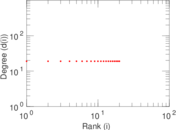
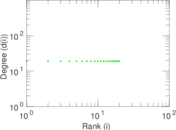
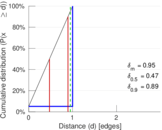
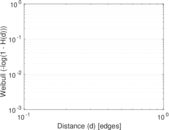
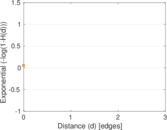
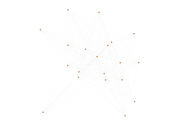
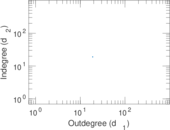
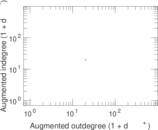
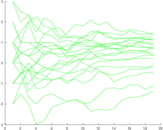
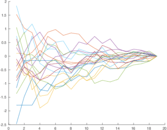
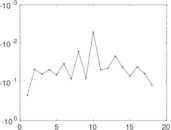
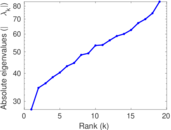
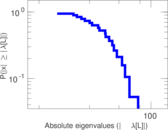
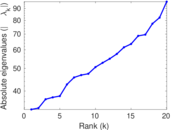
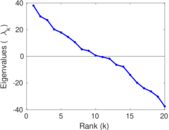
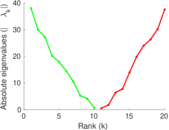
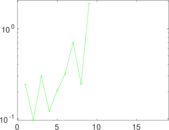
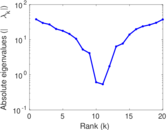
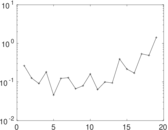
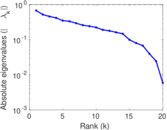
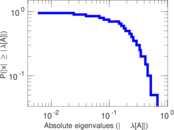
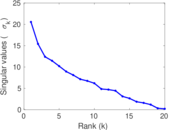
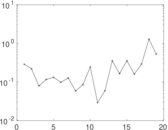
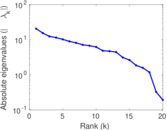
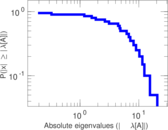
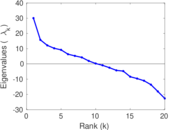
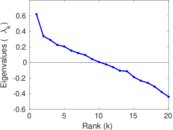
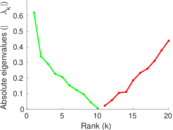
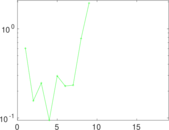
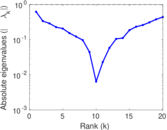
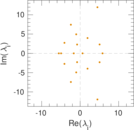
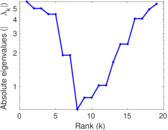
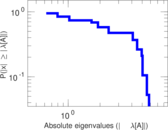
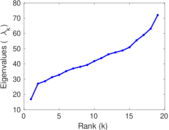
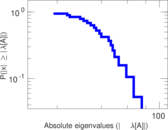
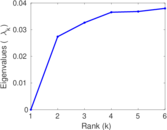
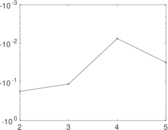
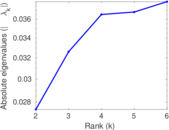
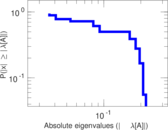
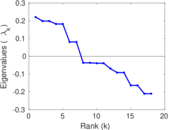
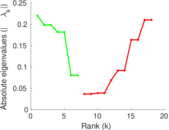
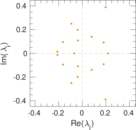
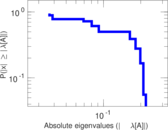
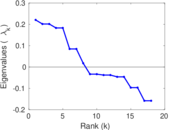
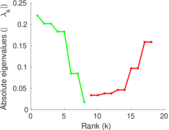
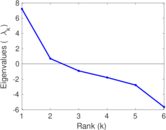
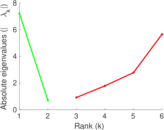
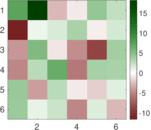
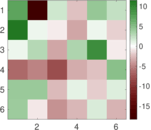
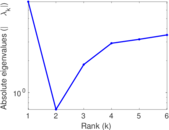
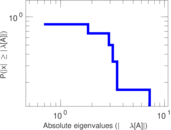
These are results of football games in France from the Ligue 1 in the season 2016/2017, in form of a directed, signed graph. Nodes are teams, and each directed edge from A to B denotes that team A played at home against team B. The edge weights are the goal difference, and thus positive if the home team wins, negative when the away team wins, and zero for a draw. The exact game results are not represented; only the goal differences are. The data was copied by hand from Wikipedia.

Metadata

Codef6
Internal nameleague-fr1-2016
NameLigue 1 (2016/2017)
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Interaction network
Dataset timestamp 2016 ⋯ 2017
Node meaningTeam
Edge meaningGame
Network formatUnipartite, directed
Edge typeSigned, possibly weighted, multiple edges
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsDoes not contain loops
Skew-symmetry Inverted edges can be interpreted as negated edges
Complete Edges exist between all possible nodes
Zero weights Edges may have weight zero

Statistics

Size n =20
Volume m =380
Unique edge count m̿ =285
Loop count l =0
Wedge count s =3,420
Claw count z =71,867
Cross count x =476,146
Triangle count t =1,140
Square count q =11,380
4-Tour count T4 =103,522
Maximum degree dmax =38
Maximum outdegree d+max =19
Maximum indegree d−max =19
Average degree d =38.000 0
Fill p =0.750 000
Average edge multiplicity m̃ =1.333 33
Size of LCC N =20
Size of LSCC Ns =20
Relative size of LSCC Nrs =1.000 00
Diameter δ =1
50-Percentile effective diameter δ0.5 =0.473 333
90-Percentile effective diameter δ0.9 =0.894 667
Median distance δM =1
Mean distance δm =0.949 367
Gini coefficient G =0.062 105 3
Balanced inequality ratio P =0.452 632
Outdegree balanced inequality ratio P+ =0.435 088
Indegree balanced inequality ratio P− =0.435 088
Relative edge distribution entropy Her =0.997 997
Power law exponent γ =20.735 6
Tail power law exponent γt =8.991 00
Tail power law exponent with p γ3 =8.991 00
p-value p =0.010 000 0
Outdegree tail power law exponent with p γ3,o =8.991 00
Outdegree p-value po =0.293 000
Indegree tail power law exponent with p γ3,i =8.721 00
Indegree p-value pi =0.881 000
Degree assortativity ρ =−0.082 908 1
Degree assortativity p-value pρ =0.117 371
In/outdegree correlation ρ± =−0.103 518
Clustering coefficient c =1.000 00
Directed clustering coefficient c± =0.764 982
Spectral norm α =22.991 2
Operator 2-norm ν =21.451 8
Cyclic eigenvalue π =4.482 24
Algebraic connectivity a =34.432 6
Spectral separation |λ1[A] / λ2[A]| =1.191 73
Reciprocity y =0.743 860
Non-bipartivity bA =0.797 627
Normalized non-bipartivity bN =0.846 165
Algebraic non-bipartivity χ =14.544 9
Spectral bipartite frustration bK =0.203 142
Negativity ζ =0.347 368
Algebraic conflict ξ =16.692 0
Triadic conflict τ =0.470 016
Spectral signed frustration φ =0.366 052
Controllability C =0
Relative controllability Cr =0.000 00

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

In/outdegree scatter plot

Item rating evolution

Edge weight/multiplicity distribution

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

Matrix decompositions plots

Downloads

References

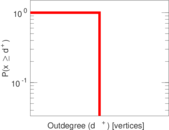
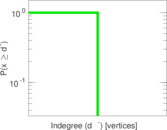
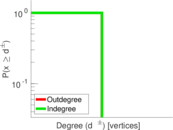
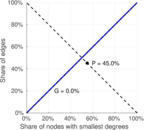
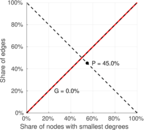
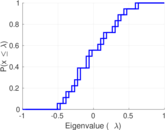
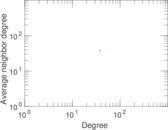
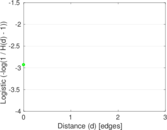
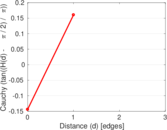
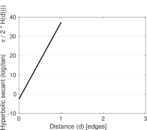
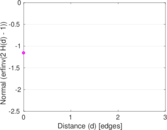
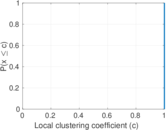
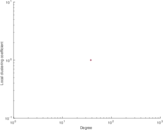
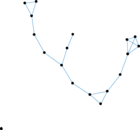
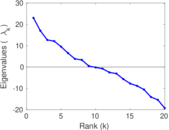
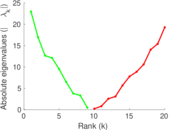
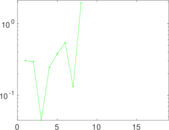
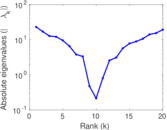
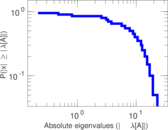
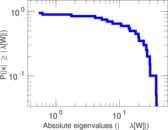
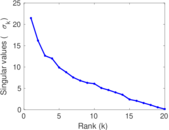
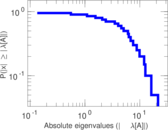
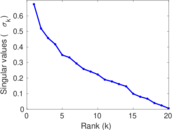
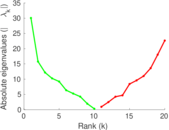
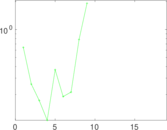
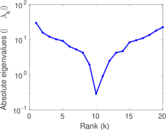
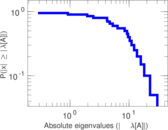
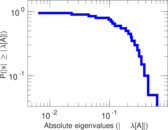
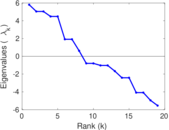
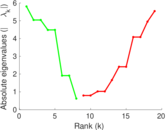
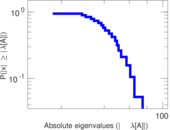
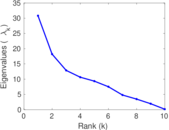
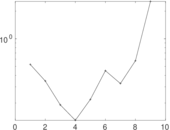
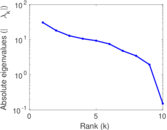
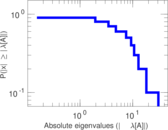
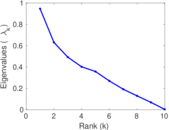
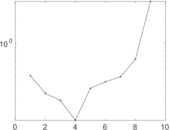
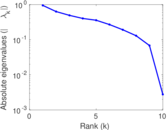
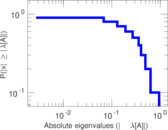
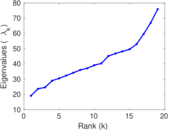
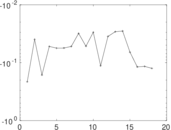
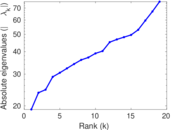
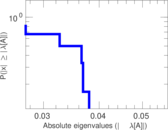
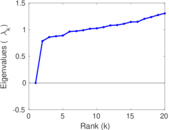
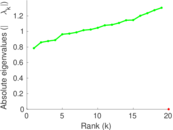
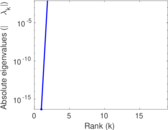
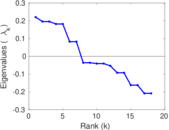
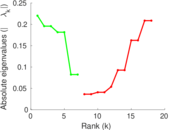
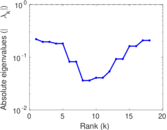
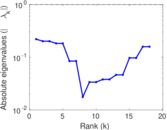
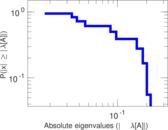
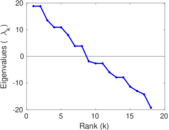
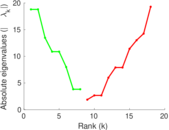
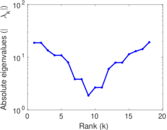
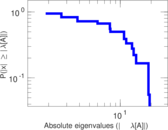
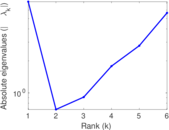
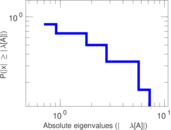
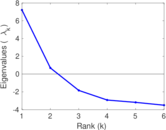
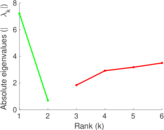
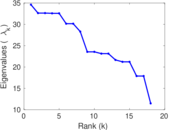
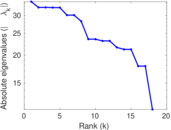
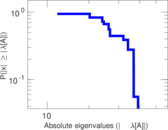
[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Michaël Fanuel and Johan A. K. Suykens. Deformed Laplacians and spectral ranking in directed networks. Applied and Computational Harmonic Analysis, 2017. In press.