Reality Mining

This undirected network contains human contact data among 100 students of the Massachusetts Institute of Technology (MIT), collected by the Reality Mining experiment performed in 2004 as part of the Reality Commons project. The data was collected over 9 months using 100 mobile phones. A node represents a person; an edge indicates that the corresponding nodes had physical contact.

Metadata

CodeRM
Internal namemit
NameReality Mining
Data sourcehttp://realitycommons.media.mit.edu/realitymining.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Human contact network
Node meaningPerson
Edge meaningContact
Network formatUnipartite, undirected
Edge typeUnweighted, multiple edges
Temporal data Edges are annotated with timestamps
LoopsDoes not contain loops

Statistics

Size n =96
Volume m =1,086,404
Unique edge count m̿ =2,539
Wedge count s =149,335
Claw count z =3,073,975
Cross count x =48,933,259
Triangle count t =36,108
Square count q =1,534,878
4-Tour count T4 =12,881,442
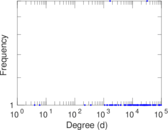
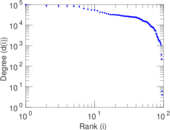
Maximum degree dmax =98,257
Average degree d =22,633.4
Fill p =0.556 798
Average edge multiplicity m̃ =427.887
Size of LCC N =96
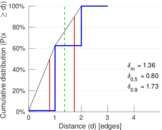
Diameter δ =3
50-Percentile effective diameter δ0.5 =0.795 737
90-Percentile effective diameter δ0.9 =1.733 01
Median distance δM =1
Mean distance δm =1.363 27
Relative edge distribution entropy Her =0.982 596
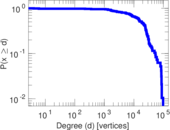
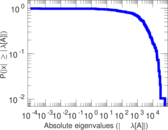
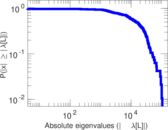
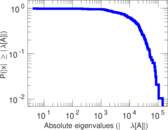
Power law exponent γ =1.317 13
Tail power law exponent γt =2.611 00
Tail power law exponent with p γ3 =2.611 00
p-value p =0.000 00
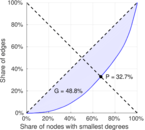
Degree assortativity ρ =−0.055 486 2
Degree assortativity p-value pρ =7.620 70 × 10−5
Clustering coefficient c =0.725 376
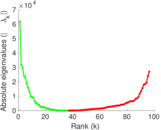
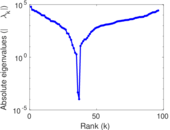
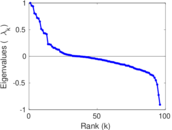
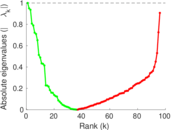
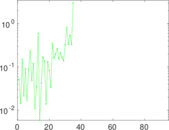
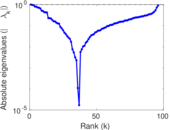
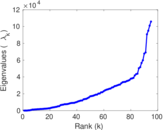
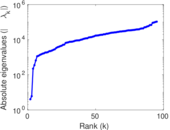
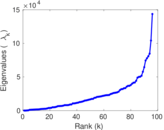
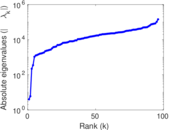
Spectral norm α =61,801.9
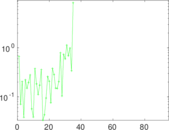
Algebraic connectivity a =4.041 03
Spectral separation |λ1[A] / λ2[A]| =1.950 75
Non-bipartivity bA =0.563 644
Normalized non-bipartivity bN =0.783 795
Algebraic non-bipartivity χ =1.973 50
Spectral bipartite frustration bK =0.009 327 28
Controllability C =1
Relative controllability Cr =0.010 416 7

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Edge weight/multiplicity distribution

Clustering coefficient distribution

Average neighbor degree distribution

Temporal distribution

Temporal hop distribution

Diameter/density evolution

Inter-event distribution

Node-level inter-event distribution

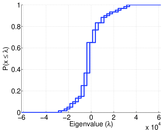
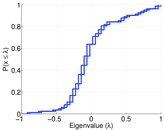
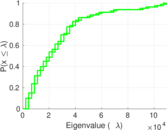
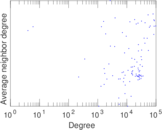
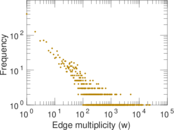
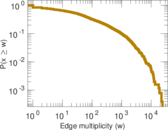
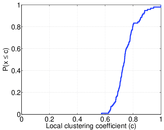
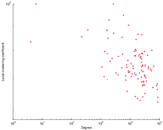
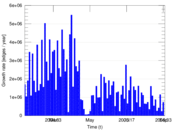
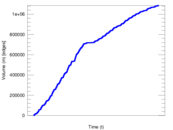
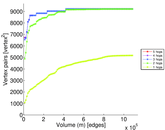
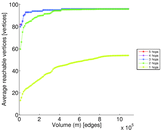
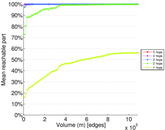
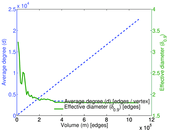
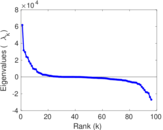
Matrix decompositions plots

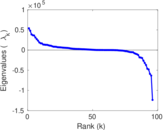
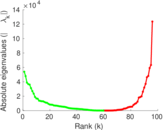
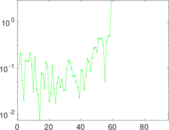
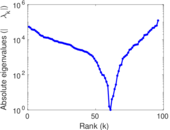
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Nathan Eagle and Alex (Sandy) Pentland. Reality Mining: Sensing complex social systems. Personal Ubiquitous Comput., 10(4):255–268, 2006.