Twitter tag–item

This is a bipartite network of tag–URL relations in Twitter. Left nodes represent tags and right nodes represent URLs. An edge shows that an URL was mentioned together with a given tag in a tweet.

Metadata

Code		`Wti`
Internal name		`munmun_twitterex_ti`
Name		Twitter tag–item
Data source		http://www.public.asu.edu/~mdechoud/datasets.html
Availability		Dataset is not available for download
Consistency check		Dataset passed all tests
Category		Feature network
Dataset timestamp		2010
Node meaning		Hashtag, URL
Edge meaning		Co-occurrence
Network format		Bipartite, undirected
Edge type		Unweighted, multiple edges
Temporal data		Edges are annotated with timestamps
Snapshot		Is a snapshot and likely to not contain all data

Statistics

Size	n =	1,502,611
Left size	n₁ =	270,582
Right size	n₂ =	1,232,029
Volume	m =	2,635,885
Unique edge count	m̿ =	1,996,158
Wedge count	s =	4,418,323,415
Claw count	z =	51,877,537,933,158
Square count	q =	70,327,726
4-Tour count	T₄ =	18,239,948,076
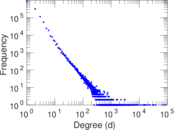
Maximum degree	d_max =	84,158
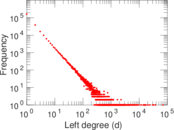
Maximum left degree	d_1max =	70,377
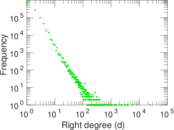
Maximum right degree	d_2max =	84,158
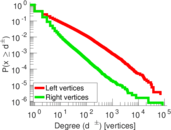
Average degree	d =	3.508 41
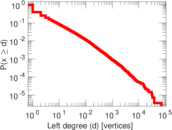
Average left degree	d₁ =	9.741 54
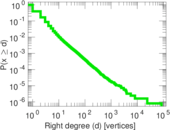
Average right degree	d₂ =	2.139 47
Fill	p =	5.987 91 × 10⁻⁶
Average edge multiplicity	m̃ =	1.320 48
Size of LCC	N =	1,234,934
Diameter	δ =	31
50-Percentile effective diameter	δ_0.5 =	5.383 58
90-Percentile effective diameter	δ_0.9 =	7.672 44
Median distance	δ_M =	6
Mean distance	δ_m =	5.911 57
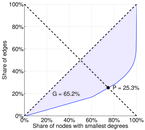
Gini coefficient	G =	0.671 119
Balanced inequality ratio	P =	0.244 057
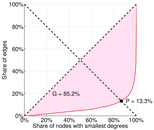
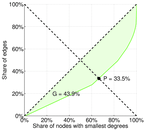
Left balanced inequality ratio	P₁ =	0.133 490
Right balanced inequality ratio	P₂ =	0.335 298
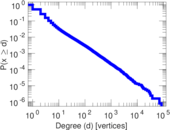
Power law exponent	γ =	3.792 46
Tail power law exponent	γ_t =	1.941 00
Degree assortativity	ρ =	−0.036 948 5
Degree assortativity p-value	p_ρ =	0.000 00
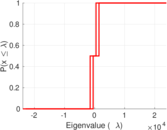
Spectral norm	α =	23,853.3
Algebraic connectivity	a =	0.000 301 907
Spectral separation	\|λ₁[A] / λ₂[A]\| =	2.926 07
Controllability	C =	1,040,405
Relative controllability	C_r =	0.692 398

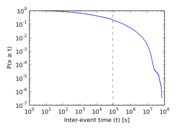
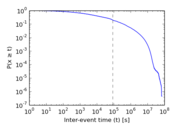
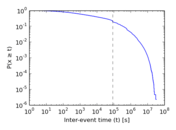
Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Hop distribution

Delaunay graph drawing

Edge weight/multiplicity distribution

Temporal distribution

Diameter/density evolution

Inter-event distribution

Node-level inter-event distribution

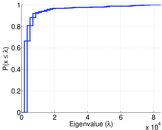
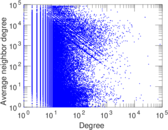
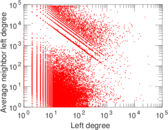
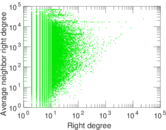
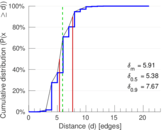
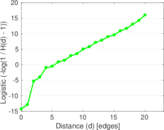
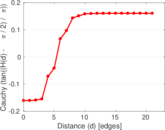
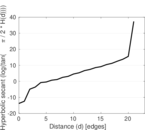
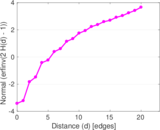
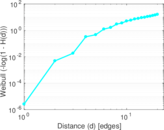
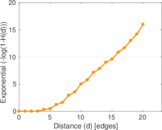
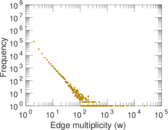
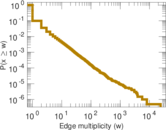
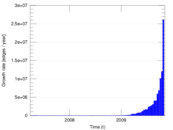
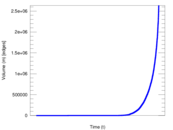
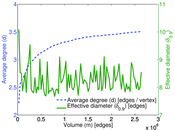
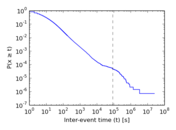
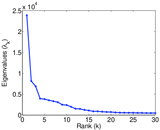
Matrix decompositions plots

Downloads

Original dataset source
KONECT extraction code (GitHub)

References

[1]	Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2]	Munmun De Choudhury, Yu-Ru Lin, Hari Sundaram, K. Selçuk Candan, Lexing Xie, and Aisling Kelliher. How does the data sampling strategy impact the discovery of information diffusion in social media? In ICWSM, pages 34–41, 2010.