SAP forums
This network contains SAP forum topics and replies. The edges are directed and
unweighted, going from the responding user to the user who created the topic.
Metadata
Statistics
| Size | n = | 29,714
|
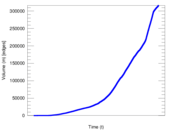
| Volume | m = | 316,266
|
| Unique edge count | m̿ = | 165,185
|
| Loop count | l = | 31,707
|
| Wedge count | s = | 20,540,914
|
| Claw count | z = | 33,525,136,262
|
| Cross count | x = | 34,767,043,592,978
|
| Triangle count | t = | 257,803
|
| Square count | q = | 21,803,510
|
| 4-Tour count | T4 = | 256,822,948
|
| Maximum degree | dmax = | 29,766
|
| Maximum outdegree | d+max = | 20,480
|
| Maximum indegree | d−max = | 9,286
|
| Average degree | d = | 21.287 3
|
| Fill | p = | 0.000 187 089
|
| Average edge multiplicity | m̃ = | 1.914 62
|
| Size of LCC | N = | 28,455
|
| Size of LSCC | Ns = | 15,879
|
| Relative size of LSCC | Nrs = | 0.534 395
|
| Diameter | δ = | 16
|
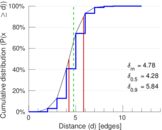
| 50-Percentile effective diameter | δ0.5 = | 4.277 96
|
| 90-Percentile effective diameter | δ0.9 = | 5.835 03
|
| Median distance | δM = | 5
|
| Mean distance | δm = | 4.778 45
|
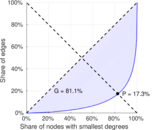
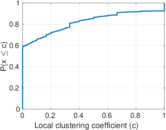
| Gini coefficient | G = | 0.810 567
|
| Balanced inequality ratio | P = | 0.172 831
|
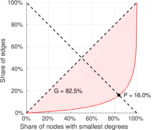
| Outdegree balanced inequality ratio | P+ = | 0.159 856
|
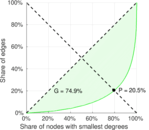
| Indegree balanced inequality ratio | P− = | 0.204 897
|
| Relative edge distribution entropy | Her = | 0.861 872
|
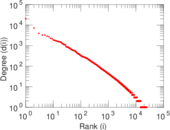
| Power law exponent | γ = | 1.874 83
|
| Tail power law exponent | γt = | 2.271 00
|
| Tail power law exponent with p | γ3 = | 2.271 00
|
| p-value | p = | 0.464 000
|
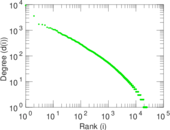
| Outdegree tail power law exponent with p | γ3,o = | 2.061 00
|
| Outdegree p-value | po = | 0.094 000 0
|
| Indegree tail power law exponent with p | γ3,i = | 2.691 00
|
| Indegree p-value | pi = | 0.566 000
|
| Degree assortativity | ρ = | −0.104 604
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.788 544
|
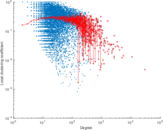
| Clustering coefficient | c = | 0.037 652 1
|
| Directed clustering coefficient | c± = | 0.036 019 4
|
| Spectral norm | α = | 1,490.72
|
| Operator 2-norm | ν = | 922.825
|
| Cyclic eigenvalue | π = | 695.387
|
| Algebraic connectivity | a = | 0.027 570 1
|
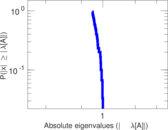
| Spectral separation | |λ1[A] / λ2[A]| = | 1.208 29
|
| Reciprocity | y = | 0.544 232
|
| Non-bipartivity | bA = | 0.172 382
|
| Normalized non-bipartivity | bN = | 0.014 608 0
|
| Algebraic non-bipartivity | χ = | 0.027 325 0
|
| Spectral bipartite frustration | bK = | 0.000 784 644
|
| Controllability | C = | 12,636
|
| Relative controllability | Cr = | 0.425 254
|
Plots

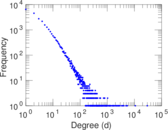
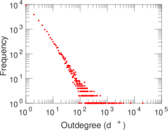
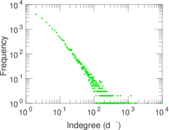
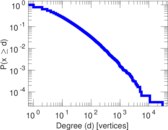
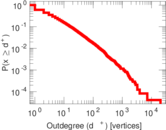
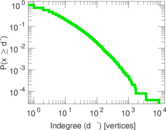
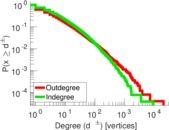
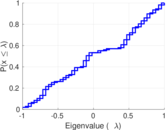
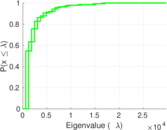
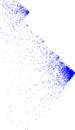
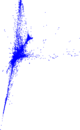
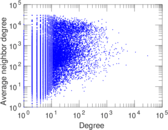

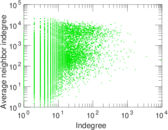
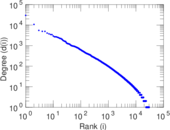
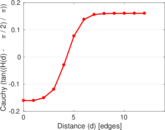
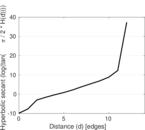
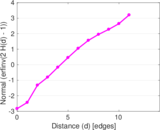
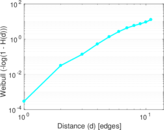
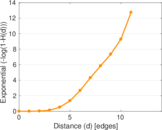



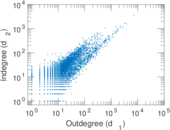
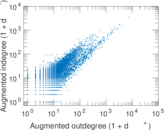
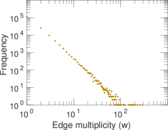
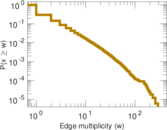
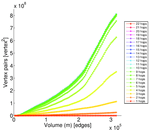
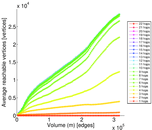
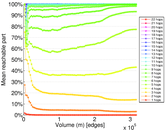
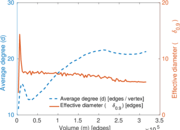

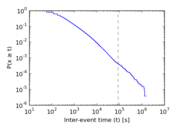
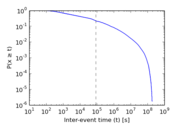
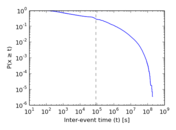
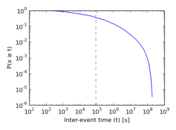
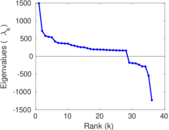
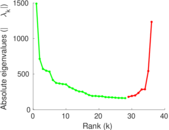
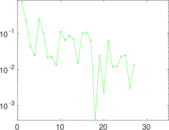
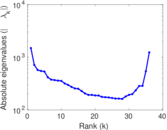
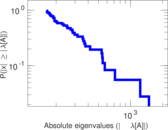
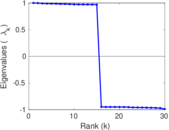
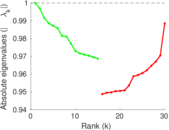
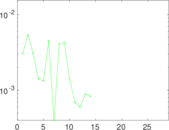
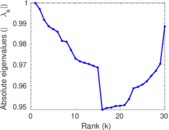
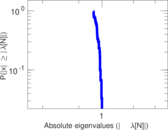
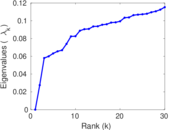
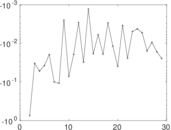
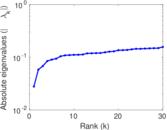
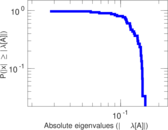
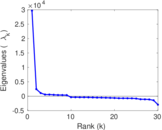
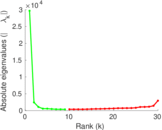
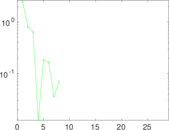
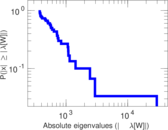
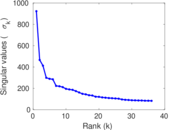
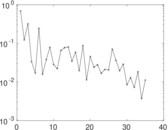
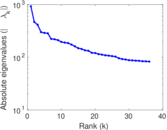
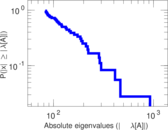
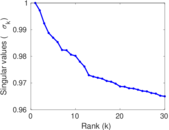
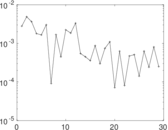
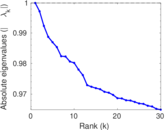
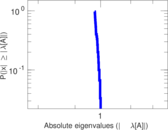
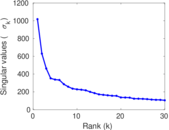
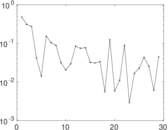
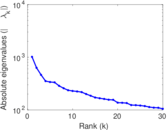
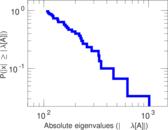
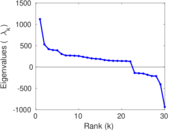
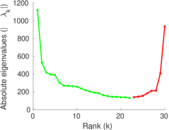
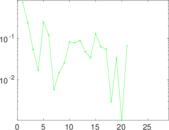
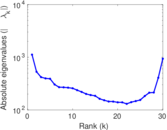
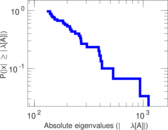
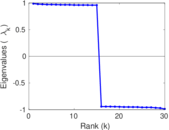
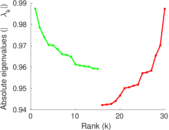
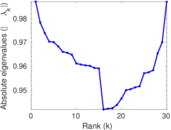
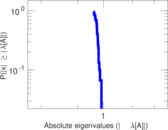
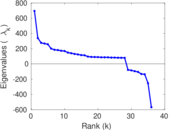
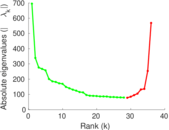
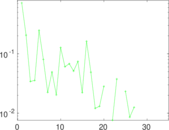
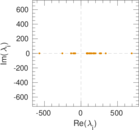
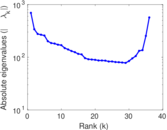
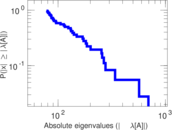
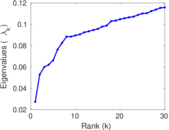
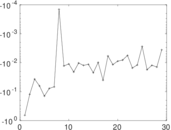
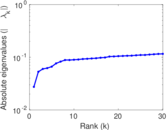
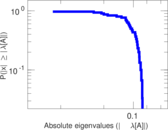
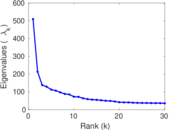
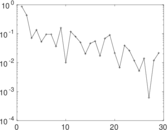
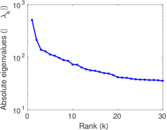
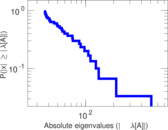
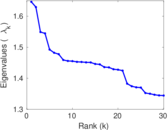
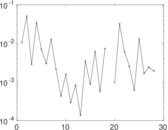
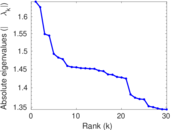
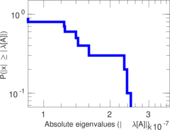
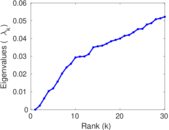
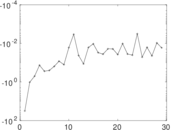
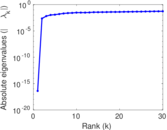
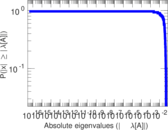
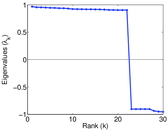
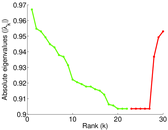
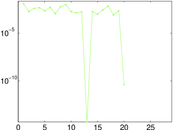
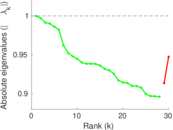
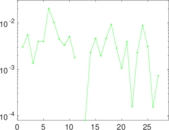
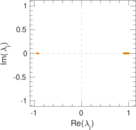
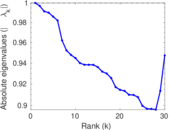
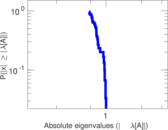
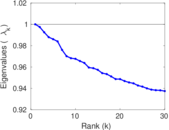
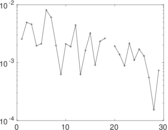
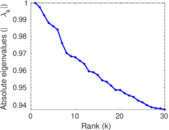
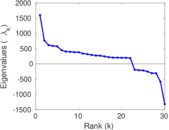
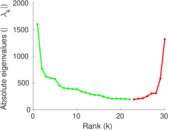
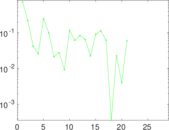
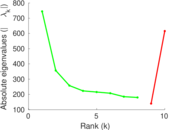
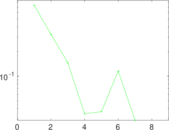
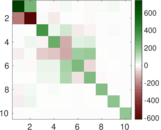
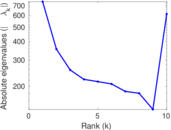
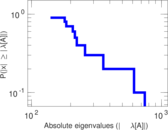
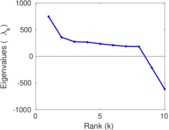
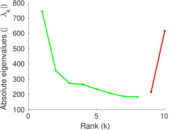
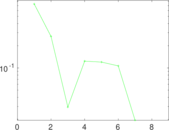
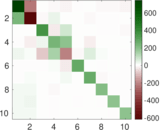
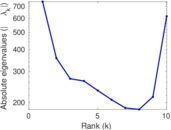
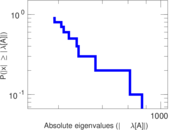
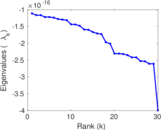
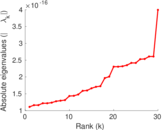
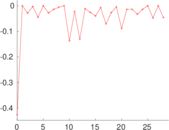
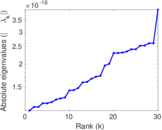
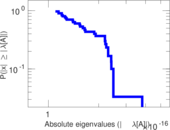
Matrix decompositions plots
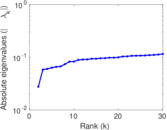
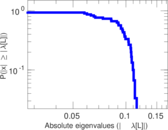
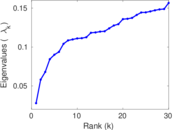
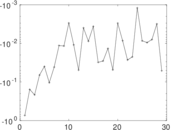


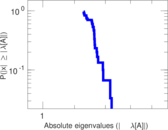
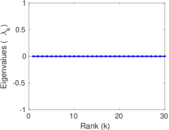
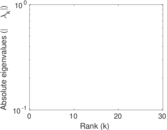
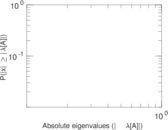
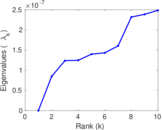
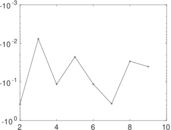
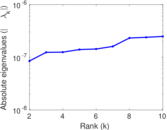
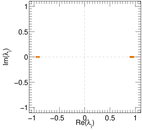
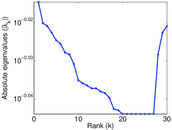
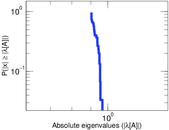
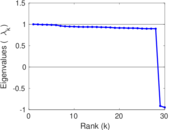
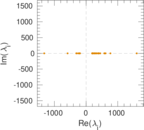
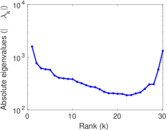
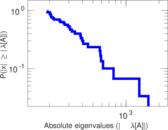
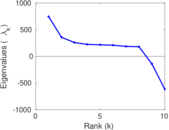
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee