MathOverflow
These are interactions from the StackExchange site "MathOverflow". The network
is between users, and directed edges represent three types of interactions:
answering a question of another user, commenting on another user's question,
and commenting on another user's answer. The network is temporal. This
network is part of a series of network from multiple StackExchange sites.
Metadata
Statistics
| Size | n = | 24,818
|
| Volume | m = | 506,550
|
| Unique edge count | m̿ = | 239,978
|
| Loop count | l = | 116,109
|
| Wedge count | s = | 54,999,653
|
| Claw count | z = | 31,659,979,718
|
| Cross count | x = | 12,853,869,969,792
|
| Triangle count | t = | 1,403,919
|
| Square count | q = | 185,375,938
|
| 4-Tour count | T4 = | 1,703,382,088
|
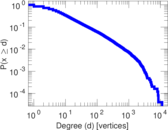
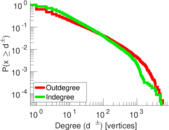
| Maximum degree | dmax = | 11,309
|
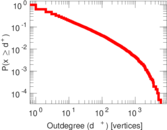
| Maximum outdegree | d+max = | 5,931
|
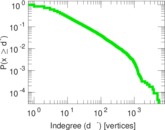
| Maximum indegree | d−max = | 5,378
|
| Average degree | d = | 40.821 2
|
| Fill | p = | 0.000 389 617
|
| Average edge multiplicity | m̃ = | 2.110 82
|
| Size of LCC | N = | 24,668
|
| Size of LSCC | Ns = | 13,095
|
| Relative size of LSCC | Nrs = | 0.527 641
|
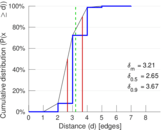
| Diameter | δ = | 9
|
| 50-Percentile effective diameter | δ0.5 = | 2.652 69
|
| 90-Percentile effective diameter | δ0.9 = | 3.668 56
|
| Median distance | δM = | 3
|
| Mean distance | δm = | 3.208 63
|
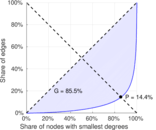
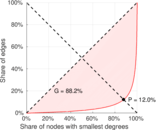
| Gini coefficient | G = | 0.854 886
|
| Balanced inequality ratio | P = | 0.143 503
|
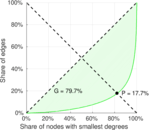
| Outdegree balanced inequality ratio | P+ = | 0.120 448
|
| Indegree balanced inequality ratio | P− = | 0.177 469
|
| Relative edge distribution entropy | Her = | 0.832 983
|
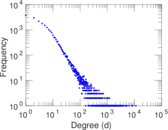
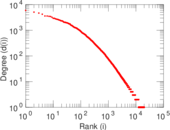
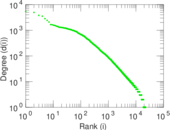
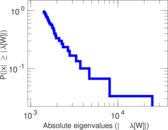
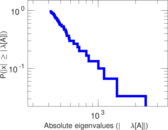
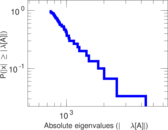
| Power law exponent | γ = | 1.682 16
|
| Tail power law exponent | γt = | 1.871 00
|
| Tail power law exponent with p | γ3 = | 1.871 00
|
| p-value | p = | 0.000 00
|
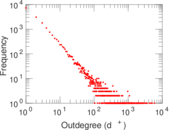
| Outdegree tail power law exponent with p | γ3,o = | 1.741 00
|
| Outdegree p-value | po = | 0.000 00
|
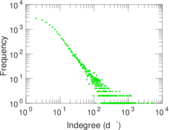
| Indegree tail power law exponent with p | γ3,i = | 2.011 00
|
| Indegree p-value | pi = | 0.000 00
|
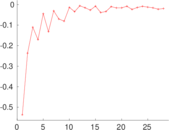
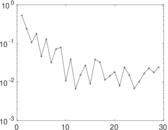
| Degree assortativity | ρ = | −0.215 181
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.796 549
|
| Clustering coefficient | c = | 0.076 577 9
|
| Directed clustering coefficient | c± = | 0.080 376 3
|
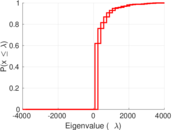
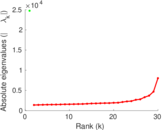
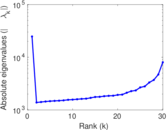
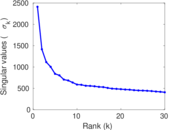
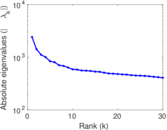
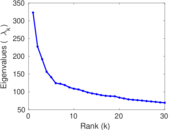
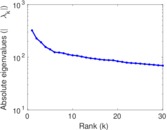
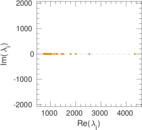
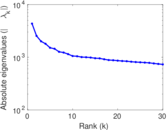
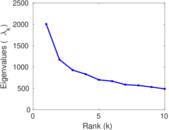
| Spectral norm | α = | 4,010.92
|
| Operator 2-norm | ν = | 2,011.89
|
| Cyclic eigenvalue | π = | 1,997.09
|
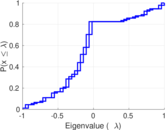
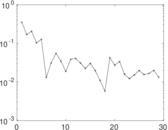
| Algebraic connectivity | a = | 0.207 313
|
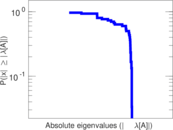
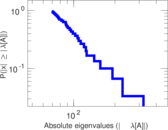
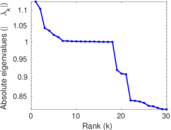
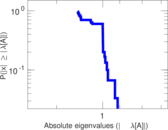
| Spectral separation | |λ1[A] / λ2[A]| = | 1.707 38
|
| Reciprocity | y = | 0.383 356
|
| Non-bipartivity | bA = | 0.994 978
|
| Normalized non-bipartivity | bN = | 0.132 313
|
| Algebraic non-bipartivity | χ = | 0.196 266
|
| Spectral bipartite frustration | bK = | 0.003 028 19
|
| Controllability | C = | 9,724
|
| Relative controllability | Cr = | 0.391 812
|
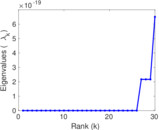
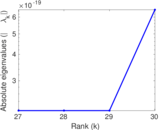
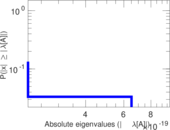
Plots

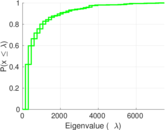
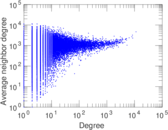
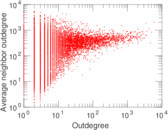
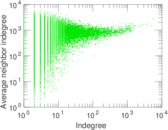
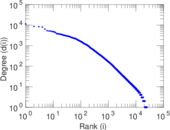
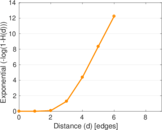



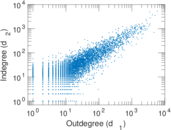
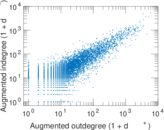
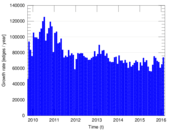
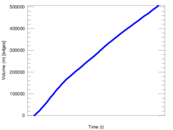
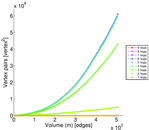
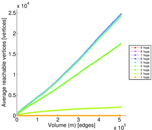
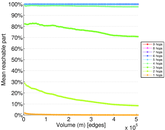
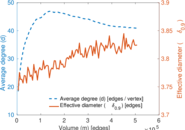

Matrix decompositions plots
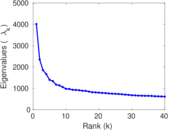
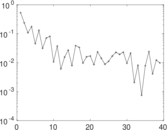
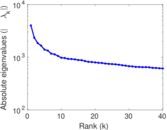
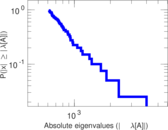
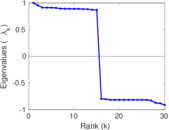
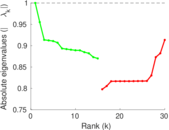
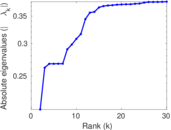
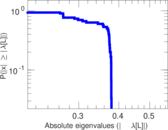
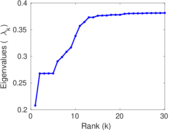
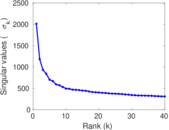
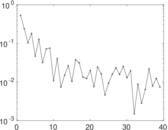
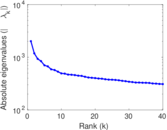
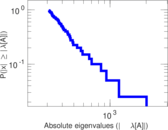
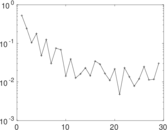
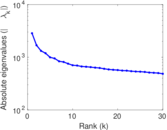
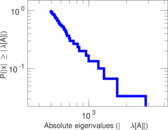
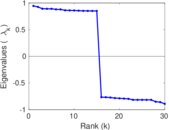
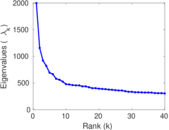
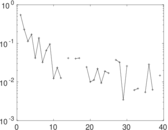
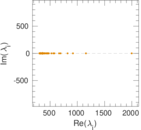
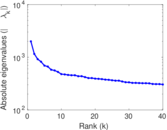
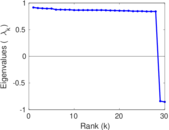
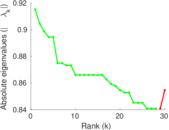
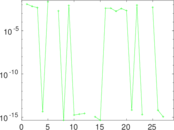
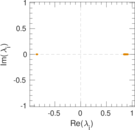
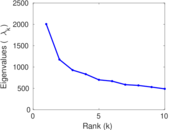
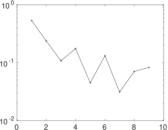
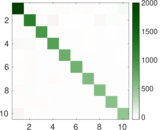
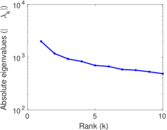
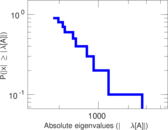
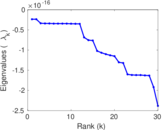
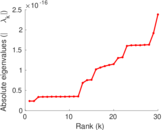
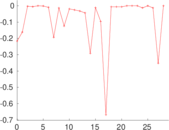
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Jure Leskovec.
Stanford Network Analysis Project.
http://snap.stanford.edu/, September 2014.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee






















































































































































