Internet topology

This is the network of connections between autonomous systems of the Internet. The nodes are autonomous systems (AS), i.e. collections of connected IP routing prefixes controlled by independent network operators. Edges are connections between autonomous systems. Multiple edges may connect two nodes, each representing an individual connection in time. Edges are annotated with the timepoint of the connection.

Metadata

CodeTO
Internal nametopology
NameInternet topology
Data sourcehttp://irl.cs.ucla.edu/topology/
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Computer network
Node meaningAutonomous system
Edge meaningConnection
Network formatUnipartite, undirected
Edge typeUnweighted, multiple edges
Temporal data Edges are annotated with timestamps
LoopsDoes not contain loops
Orientation Is not directed, but the underlying data is

Statistics

Size n =34,761
Volume m =171,403
Unique edge count m̿ =114,496
Loop count l =0
Wedge count s =34,304,301
Claw count z =20,603,857,222
Cross count x =10,997,020,148,941
Triangle count t =554,749
Square count q =79,912,964
4-Tour count T4 =776,736,356
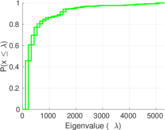
Maximum degree dmax =5,305
Average degree d =9.861 80
Fill p =0.000 189 517
Average edge multiplicity m̃ =1.497 02
Size of LCC N =34,761
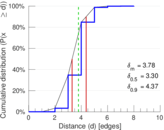
Diameter δ =10
50-Percentile effective diameter δ0.5 =3.304 83
90-Percentile effective diameter δ0.9 =4.372 41
Median distance δM =4
Mean distance δm =3.783 62
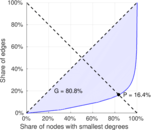
Gini coefficient G =0.808 028
Balanced inequality ratio P =0.164 131
Relative edge distribution entropy Her =0.807 662
Power law exponent γ =2.233 38
Tail power law exponent γt =1.921 00
Tail power law exponent with p γ3 =1.921 00
p-value p =0.000 00
Degree assortativity ρ =−0.214 867
Degree assortativity p-value pρ =0.000 00
Clustering coefficient c =0.048 514 2
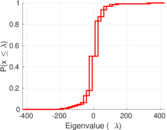
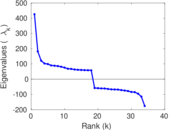
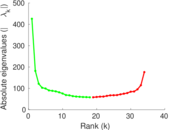
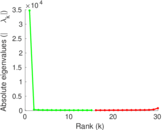
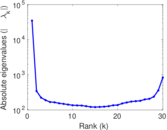
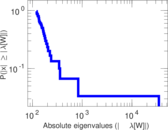
Spectral norm α =425.817
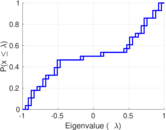
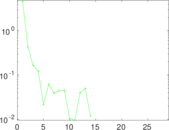
Algebraic connectivity a =0.044 087 6
Spectral separation |λ1[A] / λ2[A]| =2.341 89
Non-bipartivity bA =0.586 838
Normalized non-bipartivity bN =0.016 724 9
Algebraic non-bipartivity χ =0.032 772 5
Spectral bipartite frustration bK =0.001 321 95
Controllability C =24,439
Relative controllability Cr =0.703 058

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Edge weight/multiplicity distribution

Clustering coefficient distribution

Average neighbor degree distribution

Temporal distribution

Temporal hop distribution

Diameter/density evolution

SynGraphy

Inter-event distribution

Node-level inter-event distribution

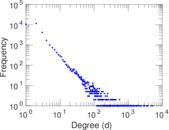
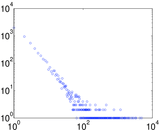
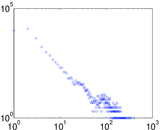
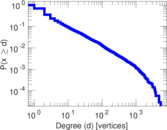
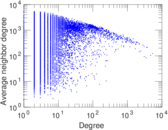
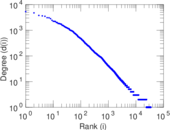
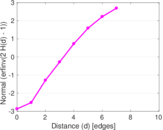
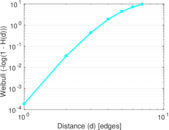
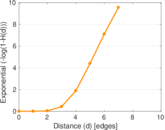
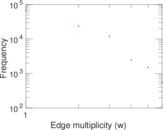
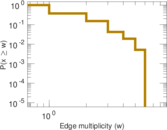
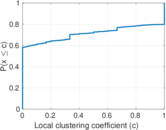
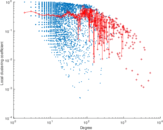
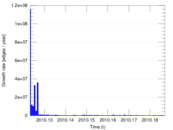
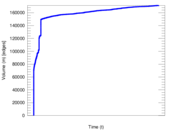
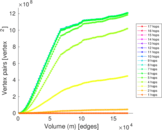
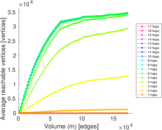
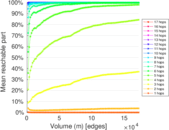
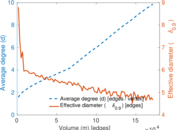
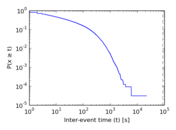
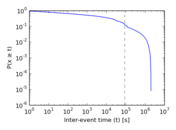
Matrix decompositions plots

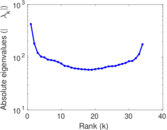
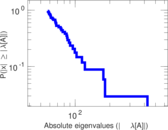
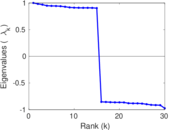
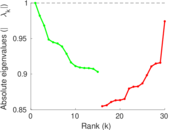
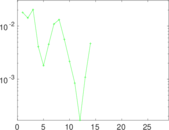
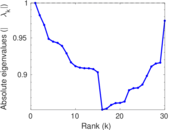
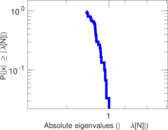
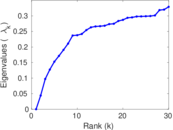
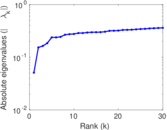
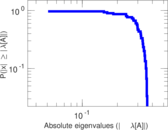
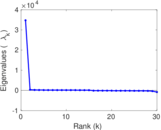
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Beichuan Zhang, Raymond Liu, Daniel Massey, and Lixia Zhang. Collecting the Internet AS-level topology. SIGCOMM Comput. Communication Review, 35(1):53–61, 2005.