Wikipedia talk (fr)
This is the communication network of the French Wikipedia. Nodes represent
users, and an edge from user A to user B denotes that user A wrote a message on
the talk page of user B at a certain timestamp.
Metadata
Statistics
| Size | n = | 1,420,367
|
| Volume | m = | 4,641,928
|
| Unique edge count | m̿ = | 2,471,501
|
| Loop count | l = | 788,289
|
| Wedge count | s = | 623,970,181,277
|
| Claw count | z = | 220,098,227,047,176,064
|
| Cross count | x = | 6.006 11 × 1022
|
| Triangle count | t = | 4,835,877
|
| Square count | q = | 11,749,091,667
|
| 4-Tour count | T4 = | 2,589,877,992,672
|
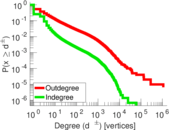
| Maximum degree | dmax = | 1,096,752
|
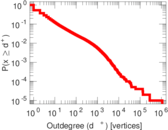
| Maximum outdegree | d+max = | 1,096,720
|
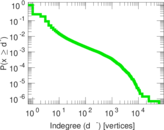
| Maximum indegree | d−max = | 60,407
|
| Average degree | d = | 6.536 24
|
| Fill | p = | 1.225 07 × 10−6
|
| Average edge multiplicity | m̃ = | 1.878 18
|
| Size of LCC | N = | 1,409,540
|
| Size of LSCC | Ns = | 56,011
|
| Relative size of LSCC | Nrs = | 0.039 434 2
|
| Diameter | δ = | 11
|
| 50-Percentile effective diameter | δ0.5 = | 1.798 42
|
| 90-Percentile effective diameter | δ0.9 = | 3.541 98
|
| Median distance | δM = | 2
|
| Mean distance | δm = | 2.592 08
|
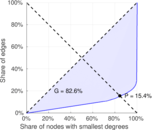
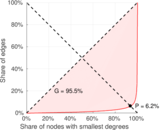
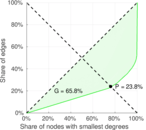
| Gini coefficient | G = | 0.825 557
|
| Balanced inequality ratio | P = | 0.153 816
|
| Outdegree balanced inequality ratio | P+ = | 0.062 284 7
|
| Indegree balanced inequality ratio | P− = | 0.237 932
|
| Relative edge distribution entropy | Her = | 0.663 160
|
| Power law exponent | γ = | 4.884 49
|
| Tail power law exponent | γt = | 2.601 00
|
| Degree assortativity | ρ = | −0.351 518
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.705 697
|
| Clustering coefficient | c = | 2.325 05 × 10−5
|
| Directed clustering coefficient | c± = | 0.025 045 3
|
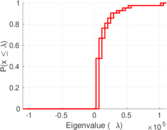
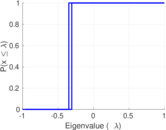
| Spectral norm | α = | 110,219
|
| Operator 2-norm | ν = | 55,109.7
|
| Cyclic eigenvalue | π = | 55,109.1
|
| Algebraic connectivity | a = | 0.024 088 0
|
| Reciprocity | y = | 0.139 799
|
| Non-bipartivity | bA = | 0.977 206
|
| Normalized non-bipartivity | bN = | 0.012 556 7
|
| Algebraic non-bipartivity | χ = | 0.024 088 3
|
| Spectral bipartite frustration | bK = | 0.001 829 73
|
| Controllability | C = | 1,351,987
|
| Relative controllability | Cr = | 0.951 858
|
Plots

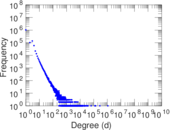
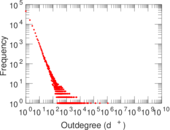
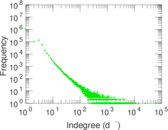
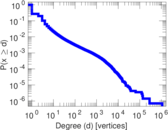
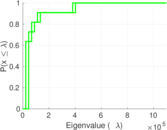



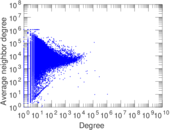
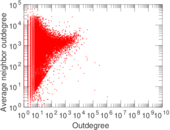
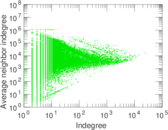
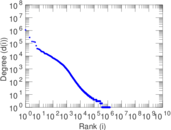
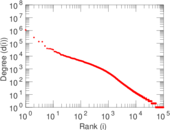
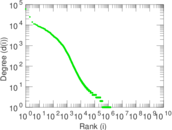
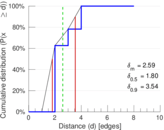
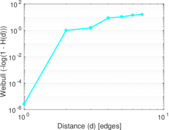
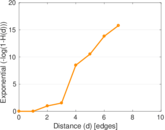
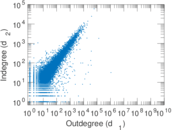
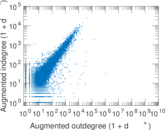

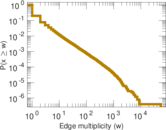
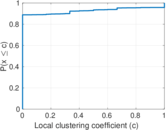
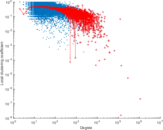
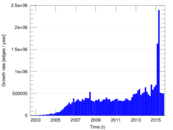
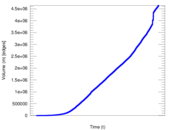
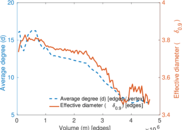
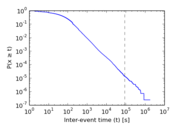
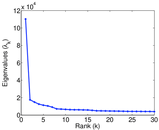
Matrix decompositions plots
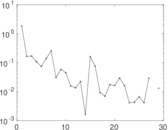
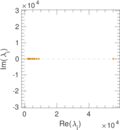
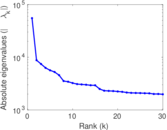

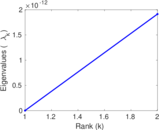
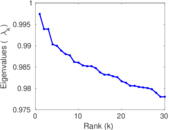
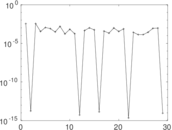
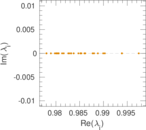
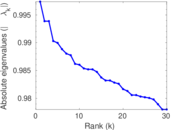

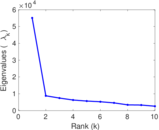
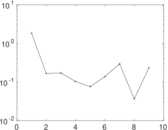
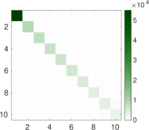
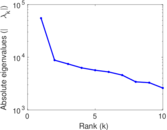

Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Jun Sun, Jérôme Kunegis, and Steffen Staab.
Predicting user roles in social networks using transfer learning with
feature transformation.
In Proc. ICDM Workshop on Data Min. in Netw., 2016.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee



































































