Wikipedia threads (de)
This is a dataset of discussion threads on the German Wikipedia. Node of the
network are users of the German Wikipedia. A directed from user A to user B
denotes that user A wrote a comment in a discussion as a reply to a comment of
user B.
Metadata
Statistics
| Size | n = | 91,340
|
| Volume | m = | 2,435,731
|
| Unique edge count | m̿ = | 987,092
|
| Loop count | l = | 384,547
|
| Wedge count | s = | 235,942,901
|
| Claw count | z = | 189,512,901,727
|
| Cross count | x = | 90,906,845,815,278
|
| Triangle count | t = | 5,727,265
|
| Square count | q = | 1,088,430,251
|
| 4-Tour count | T4 = | 9,652,669,352
|
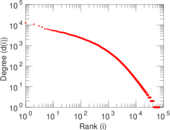
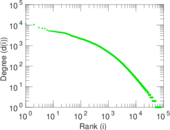
| Maximum degree | dmax = | 24,285
|
| Maximum outdegree | d+max = | 12,787
|
| Maximum indegree | d−max = | 11,498
|
| Average degree | d = | 53.333 3
|
| Fill | p = | 0.000 118 314
|
| Average edge multiplicity | m̃ = | 2.467 58
|
| Size of LCC | N = | 89,146
|
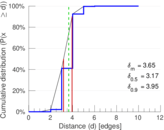
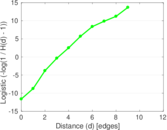
| Diameter | δ = | 13
|
| 50-Percentile effective diameter | δ0.5 = | 3.172 52
|
| 90-Percentile effective diameter | δ0.9 = | 3.951 42
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 3.645 30
|
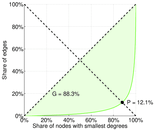
| Balanced inequality ratio | P = | 0.107 334
|
| Outdegree balanced inequality ratio | P+ = | 0.113 323
|
| Indegree balanced inequality ratio | P− = | 0.120 742
|
| Power law exponent | γ = | 1.816 00
|
| Tail power law exponent | γt = | 1.701 00
|
| Degree assortativity | ρ = | −0.064 893 0
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.911 943
|
| Clustering coefficient | c = | 0.072 821 8
|
| Directed clustering coefficient | c± = | 0.067 029 8
|
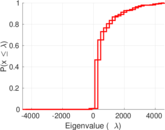
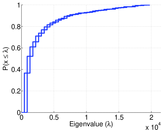
| Spectral norm | α = | 4,590.30
|
| Operator 2-norm | ν = | 2,316.66
|
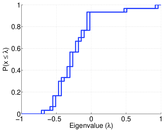
| Algebraic connectivity | a = | 0.077 071 3
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.092 91
|
| Reciprocity | y = | 0.493 334
|
| Non-bipartivity | bA = | 0.785 514
|
| Normalized non-bipartivity | bN = | 0.043 517 8
|
| Algebraic non-bipartivity | χ = | 0.073 226 5
|
| Spectral bipartite frustration | bK = | 0.001 077 10
|
| Controllability | C = | 43,028
|
| Relative controllability | Cr = | 0.471 075
|
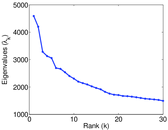
Plots



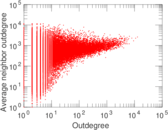
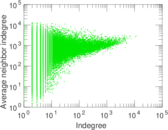
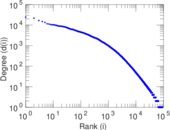
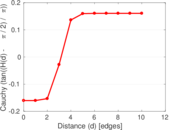
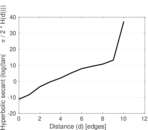
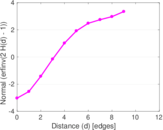
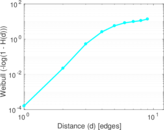
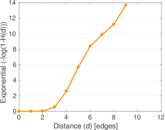
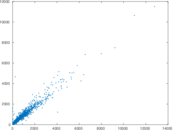
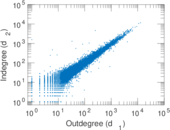
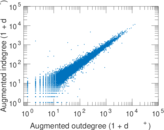
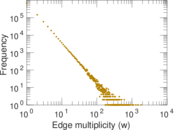
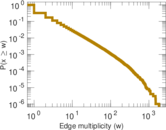
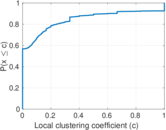
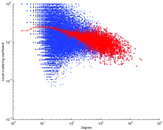
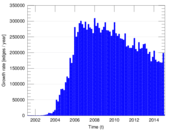
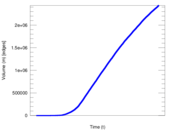
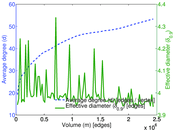

Matrix decompositions plots
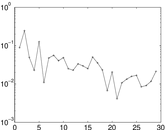
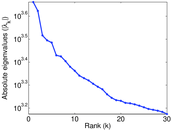
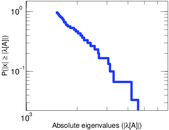
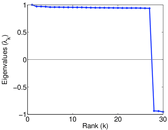
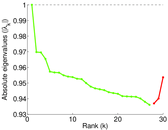
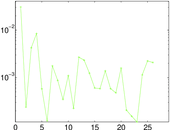
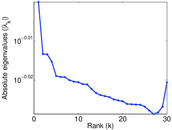
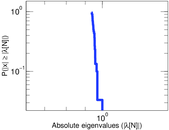
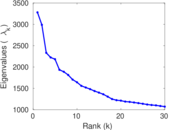
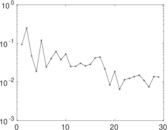
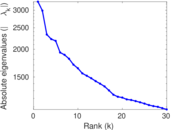
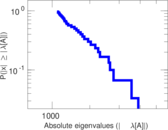
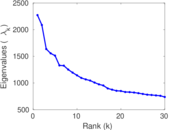
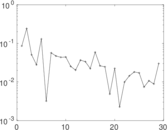
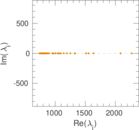
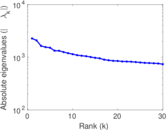
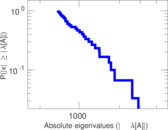
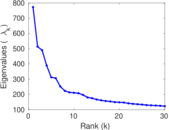
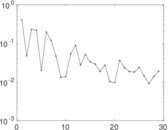
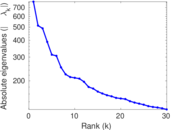
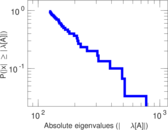
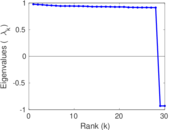
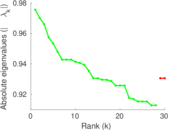
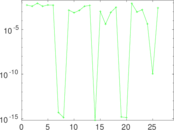
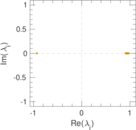
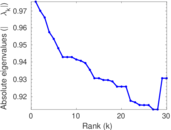
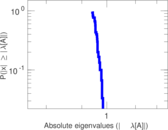
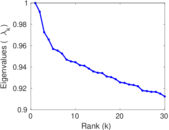
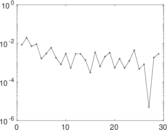
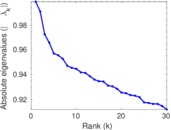
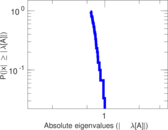
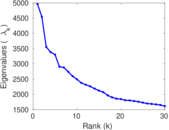
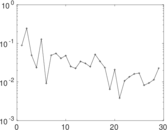
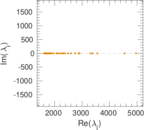
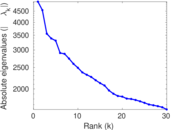
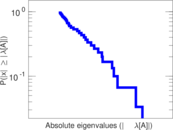
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee











































































