CiteULike user–tag

This is the bipartite network of users and tags in CiteULike. Each edge represents a tag assignment that connects a user and a tag. Since a user can assign a tag to multiple publications, the network contains multiple edges. The edges are annotated with the creation time of the tag assignment.

Metadata

CodeCut
Internal nameciteulike-ut
NameCiteULike user–tag
Data sourcehttp://www.citeulike.org/faq/data.adp
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Interaction network
Dataset timestamp 2007
Node meaningUser, tag
Edge meaningAssignment
Network formatBipartite, undirected
Edge typeUnweighted, multiple edges
Temporal data Edges are annotated with timestamps

Statistics

Size n =175,992
Left size n1 =22,715
Right size n2 =153,277
Volume m =2,411,819
Unique edge count m̿ =538,761
Wedge count s =192,371,639
Claw count z =194,428,758,411
Cross count x =302,871,675,261,597
Square count q =146,940,165
4-Tour count T4 =1,946,141,506
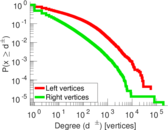
Maximum degree dmax =189,295
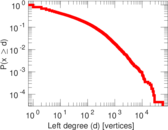
Maximum left degree d1max =57,706
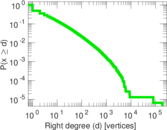
Maximum right degree d2max =189,295
Average degree d =27.408 3
Average left degree d1 =106.177
Average right degree d2 =15.735 0
Fill p =0.000 154 741
Average edge multiplicity m̃ =4.476 60
Size of LCC N =174,060
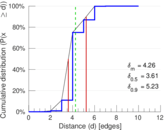
Diameter δ =12
50-Percentile effective diameter δ0.5 =3.609 05
90-Percentile effective diameter δ0.9 =5.233 56
Median distance δM =4
Mean distance δm =4.262 34
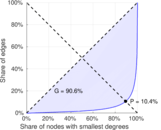
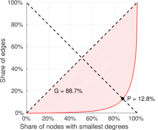
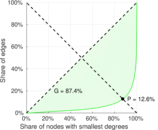
Gini coefficient G =0.912 555
Balanced inequality ratio P =0.099 462 3
Left balanced inequality ratio P1 =0.128 030
Right balanced inequality ratio P2 =0.126 018
Relative edge distribution entropy Her =0.827 610
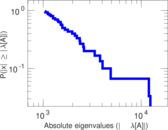
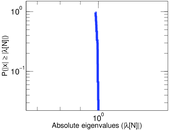
Power law exponent γ =2.821 69
Tail power law exponent γt =1.791 00
Degree assortativity ρ =−0.097 101 6
Degree assortativity p-value pρ =0.000 00
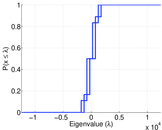
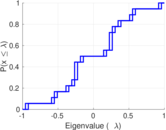
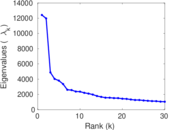
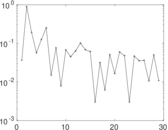
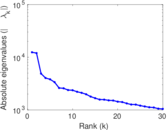
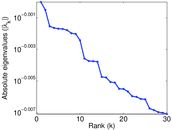
Spectral norm α =12,418.1
Algebraic connectivity a =0.031 527 5
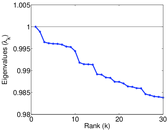
Spectral separation |λ1[A] / λ2[A]| =1.037 44
Controllability C =142,640
Relative controllability Cr =0.810 491

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Delaunay graph drawing

Edge weight/multiplicity distribution

Temporal distribution

Diameter/density evolution

Inter-event distribution

Node-level inter-event distribution

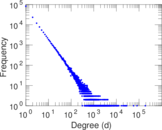
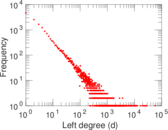
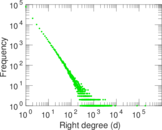
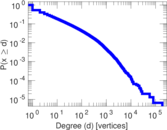
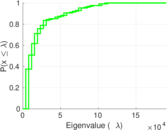
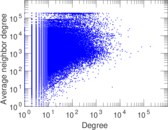
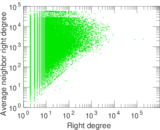
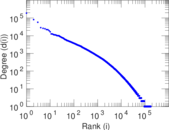
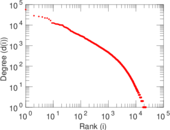
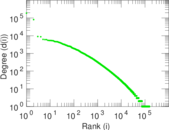
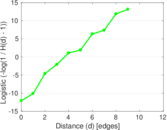
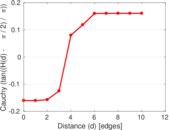
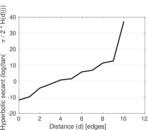
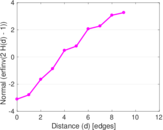
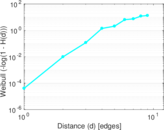
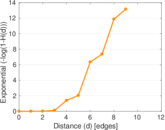
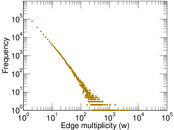
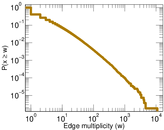
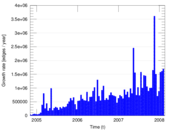
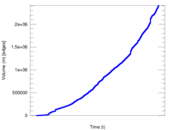
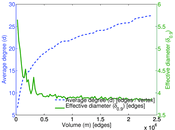
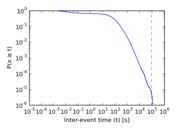
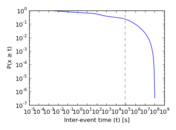
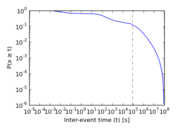
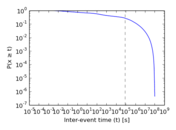
Matrix decompositions plots

Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Kevin Emamy and Richard Cameron. CiteULike: A researcher's social bookmarking service. Ariadne, (51), 2007.