CiaoDVD movie ratings
This is the bipartite user–movie rating network of the site
http://dvd.ciao.co.uk/ from 2013. The dataset contains 303 instances of
multiple edges. The timestamps are only precise up to one day.
Metadata
Statistics
| Size | n = | 33,736
|
| Left size | n1 = | 17,615
|
| Right size | n2 = | 16,121
|
| Volume | m = | 72,665
|
| Unique edge count | m̿ = | 72,345
|
| Wedge count | s = | 4,896,641
|
| Claw count | z = | 714,761,874
|
| Cross count | x = | 130,769,246,563
|
| Square count | q = | 610,909
|
| 4-Tour count | T4 = | 24,620,422
|
| Maximum degree | dmax = | 1,106
|
| Maximum left degree | d1max = | 1,106
|
| Maximum right degree | d2max = | 433
|
| Average degree | d = | 4.307 86
|
| Average left degree | d1 = | 4.125 18
|
| Average right degree | d2 = | 4.507 47
|
| Fill | p = | 0.000 254 762
|
| Average edge multiplicity | m̃ = | 1.004 42
|
| Size of LCC | N = | 32,135
|
| Diameter | δ = | 19
|
| 50-Percentile effective diameter | δ0.5 = | 4.455 73
|
| 90-Percentile effective diameter | δ0.9 = | 5.942 69
|
| Median distance | δM = | 5
|
| Mean distance | δm = | 5.000 04
|
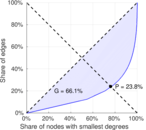
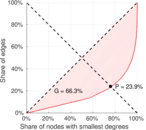
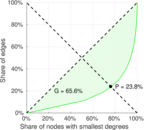
| Gini coefficient | G = | 0.611 394
|
| Balanced inequality ratio | P = | 0.266 024
|
| Left balanced inequality ratio | P1 = | 0.239 160
|
| Right balanced inequality ratio | P2 = | 0.238 897
|
| Relative edge distribution entropy | Her = | 0.884 257
|
| Power law exponent | γ = | 2.500 71
|
| Tail power law exponent | γt = | 2.541 00
|
| Tail power law exponent with p | γ3 = | 2.541 00
|
| p-value | p = | 0.434 000
|
| Left tail power law exponent with p | γ3,1 = | 2.271 00
|
| Left p-value | p1 = | 0.897 000
|
| Right tail power law exponent with p | γ3,2 = | 1.851 00
|
| Right p-value | p2 = | 0.000 00
|
| Degree assortativity | ρ = | −0.169 306
|
| Degree assortativity p-value | pρ = | 0.000 00
|
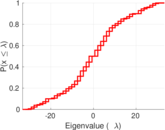
| Spectral norm | α = | 33.296 7
|
| Algebraic connectivity | a = | 9.868 54 × 10−5
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.341 77
|
| Negativity | ζ = | 0.422 172
|
| Algebraic conflict | ξ = | 0.018 375 1
|
| Spectral signed frustration | φ = | 0.001 033 49
|
| Controllability | C = | 18,998
|
| Relative controllability | Cr = | 0.563 137
|
Plots

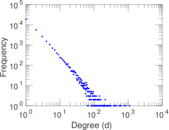
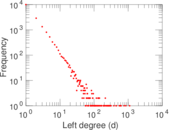
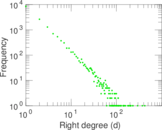
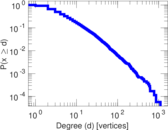
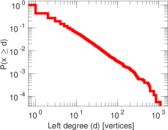
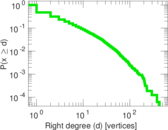
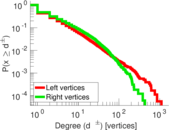
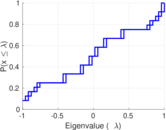
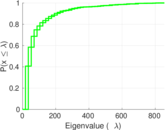

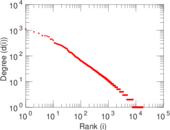
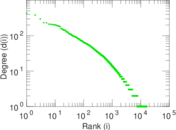
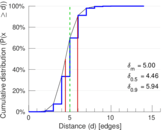
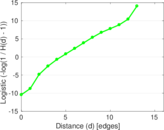
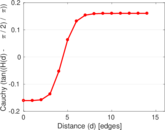
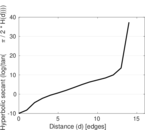
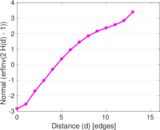
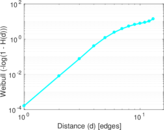
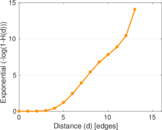


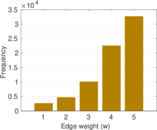
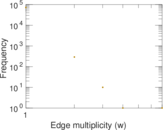
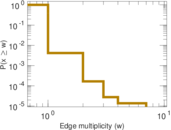
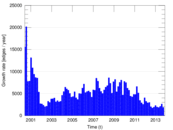
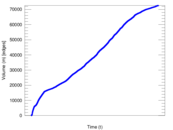
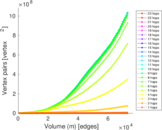
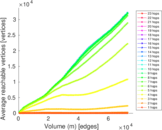
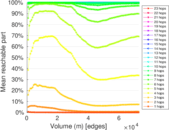
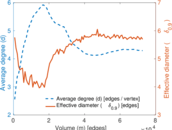
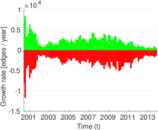
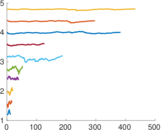
Matrix decompositions plots
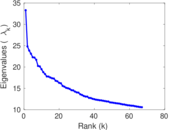
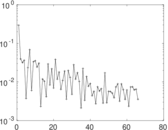
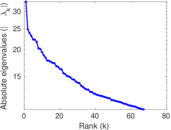
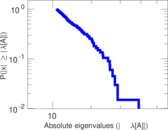
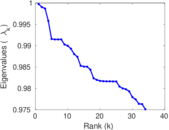
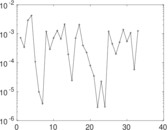
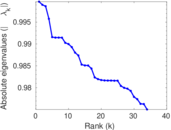
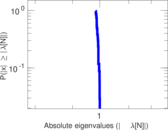
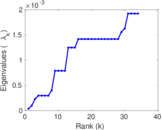
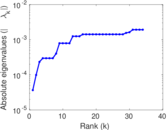
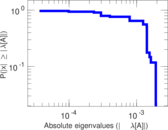
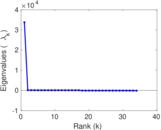
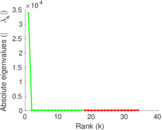
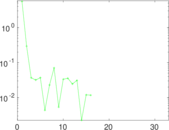
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Guobing Guo, Jie Zhang, Daniel Thalmann, and Neil Yorke-Smith.
ETAF: An extended trust antecedents framework for trust prediction.
In Proc. Int. Conf. Adv. in Soc. Netw. Anal. and Min., pages
540–547, 2014.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee