KONECT ‣ Networks ‣
Buy Me a Coffee
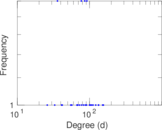
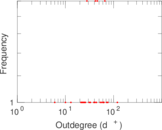
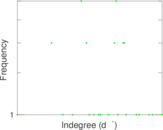
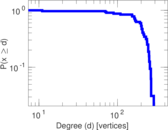
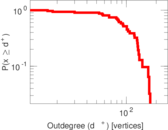
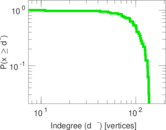
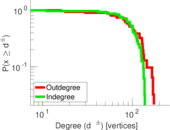
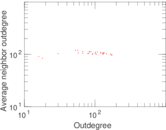
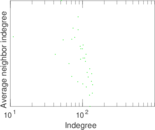
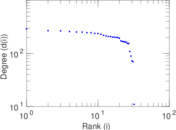
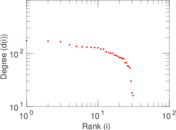
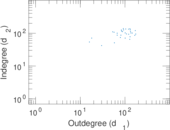
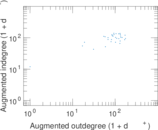
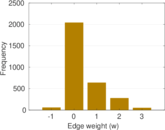
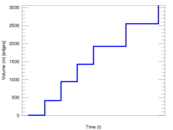
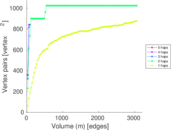
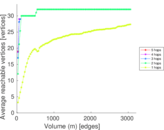
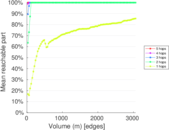
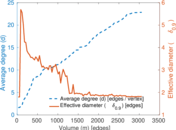
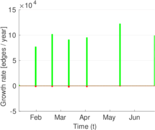
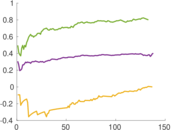
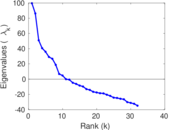
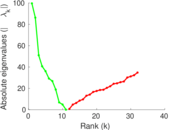
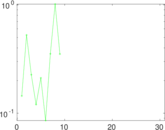
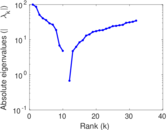
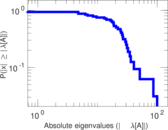
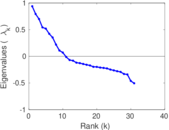
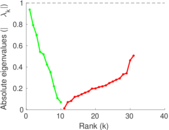
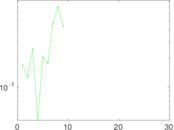
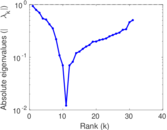
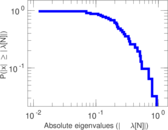
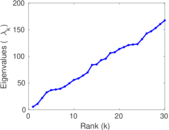
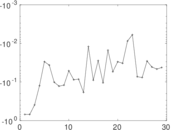
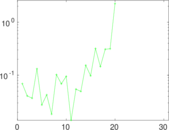
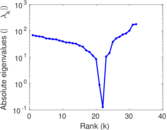
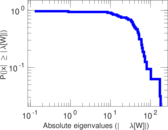
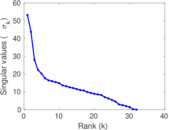
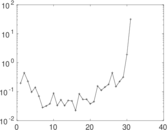
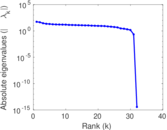
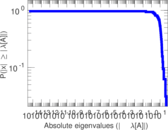
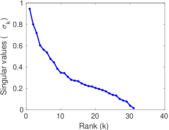
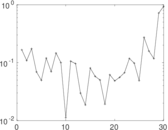
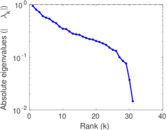
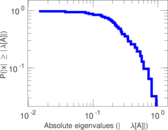
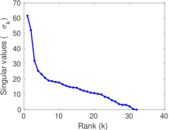
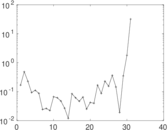
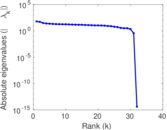
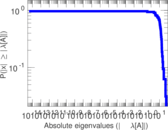
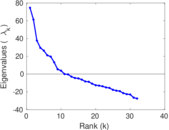
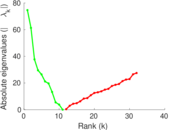
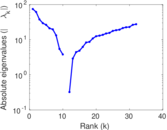
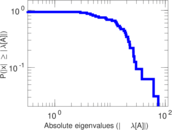
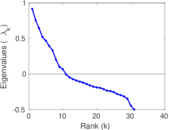
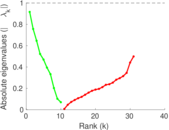
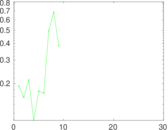
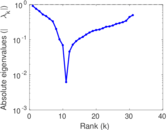
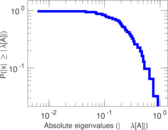
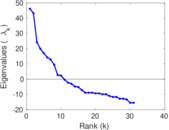
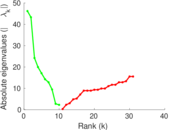
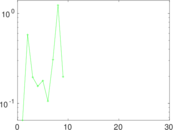
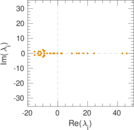
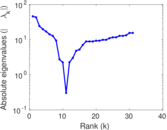
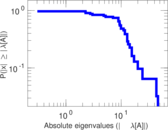
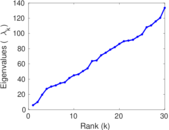
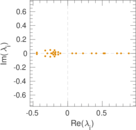
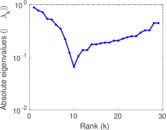
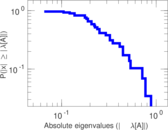
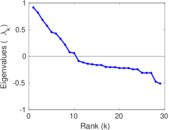
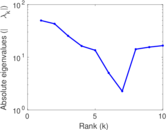
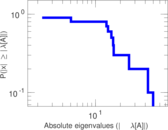
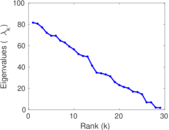
This directed network contains friendship ratings between 32 university freshmen who mostly did not know each other before starting university. Each student was asked to rate the other student at seven different time points. Note that the origin of the timestamps is not accurately known but the distance between two timestamps is correct. A node represents a student and an edge between two students shows that the left rated the right one The edge weights show how good their friendship is in the eye of the left node. The weight ranges from −1 for risk of getting into conflict to +3 for best friend.
| Code | Mv
| |
| Internal name | moreno_vdb
| |
| Name | Dutch college | |
| Data source | http://moreno.ss.uci.edu/data.html#vdb | |
| Availability |  | Dataset is available for download |
| Consistency check |  | Dataset passed all tests |
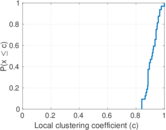
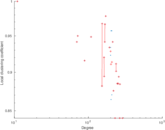
| Category | Human social network | |
| Node meaning | Student | |
| Edge meaning | Rating | |
| Network format |  | Unipartite, directed |
| Edge type |  | Signed, possibly weighted, multiple edges |
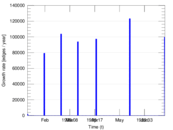
| Temporal data |  | Edges are annotated with timestamps |
| Reciprocal |  | Contains reciprocal edges |
| Directed cycles | | Contains directed cycles |
| Loops | | Does not contain loops |
| Zero weights |  | Edges may have weight zero |
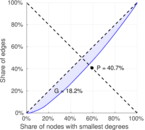
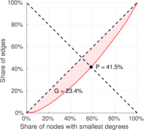
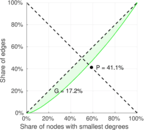
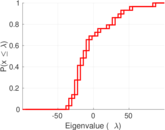
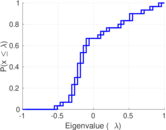
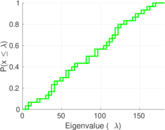
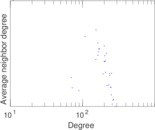
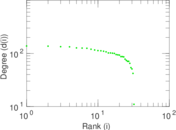
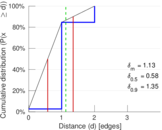
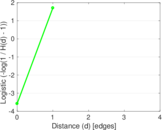
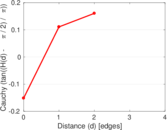
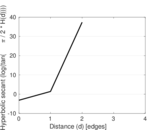
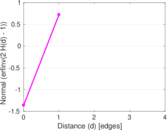
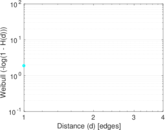
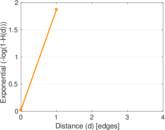
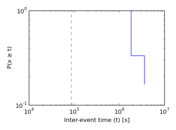
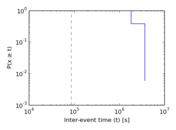
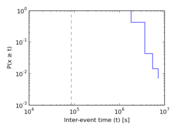
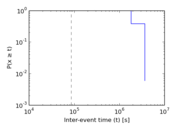
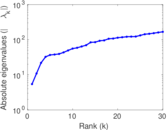
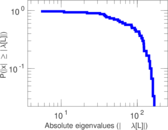
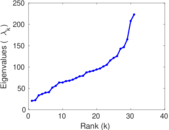
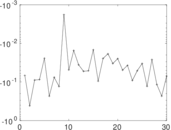
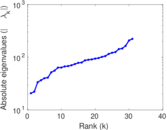
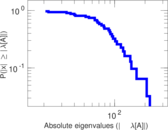
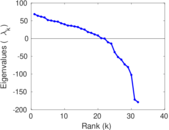
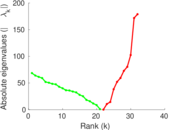
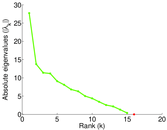
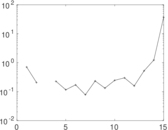
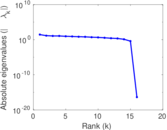
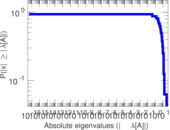
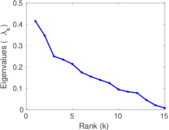
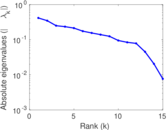
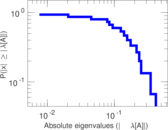
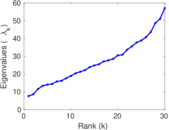
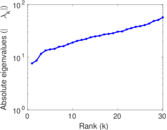
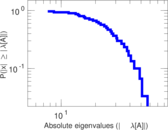
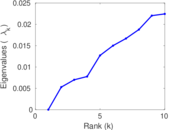
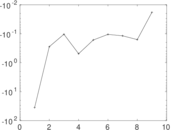
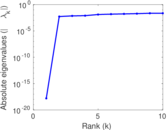
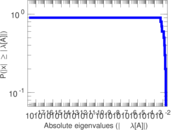
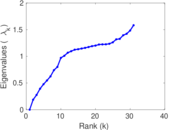
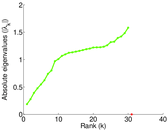
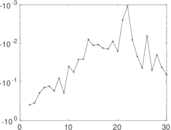
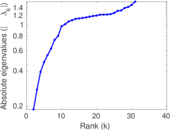
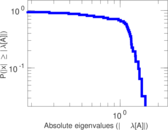
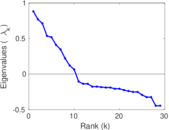
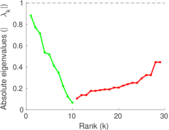
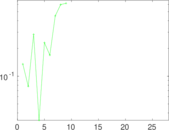
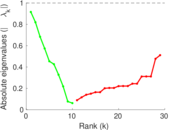
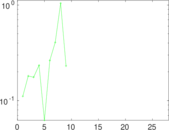
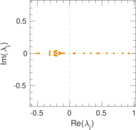
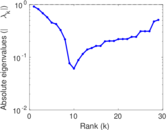
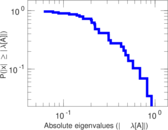
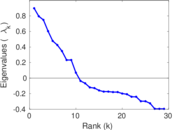
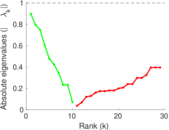
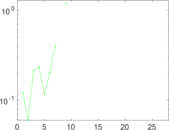
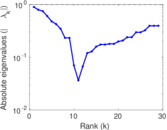
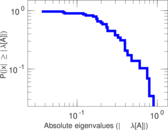
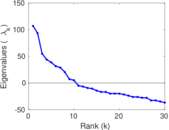
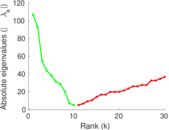
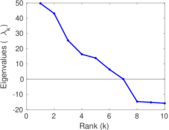
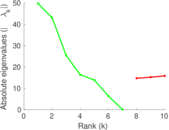
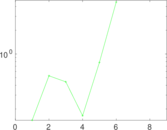
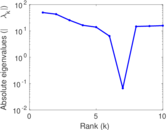
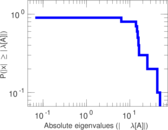
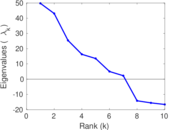
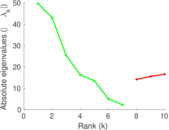
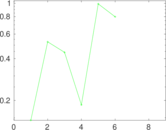
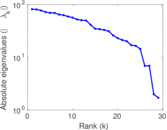
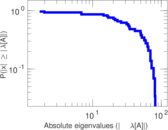
| [1] | Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ] |
| [2] | Gerhard G. Van de Bunt, Marijtje A. J. Van Duijn, and Tom A. B. Snijders. Friendship networks through time: An actor-oriented dynamic statistical network model. Comput. and Math. Organization Theory, 5(2):167–192, 1999. |