Bitcoin OTC
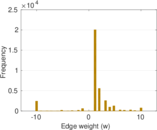
This is a user–user trust/distrust network, from the Bitcoin OTC platform, on
which Bitcoins are traded. Each directed edge represents trust or distrust on
a scale from −10 to +10. Positive edge weights denote trust, and negative
edge weights denote distrust. An edge weight of zero does not appear.
Metadata
Statistics
| Size | n = | 5,881
|
| Volume | m = | 35,592
|
| Loop count | l = | 0
|
| Wedge count | s = | 1,696,179
|
| Claw count | z = | 811,596,829
|
| Cross count | x = | 175,418,444,313
|
| Triangle count | t = | 33,493
|
| Square count | q = | 1,043,996
|
| 4-Tour count | T4 = | 15,179,668
|
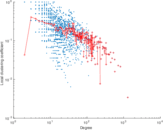
| Maximum degree | dmax = | 1,298
|
| Maximum outdegree | d+max = | 763
|
| Maximum indegree | d−max = | 535
|
| Average degree | d = | 12.104 1
|
| Fill | p = | 0.001 029 26
|
| Size of LCC | N = | 5,875
|
| Size of LSCC | Ns = | 4,709
|
| Relative size of LSCC | Nrs = | 0.800 714
|
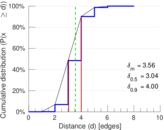
| Diameter | δ = | 9
|
| 50-Percentile effective diameter | δ0.5 = | 3.037 71
|
| 90-Percentile effective diameter | δ0.9 = | 3.996 62
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 3.558 34
|
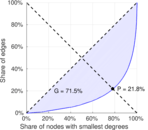
| Gini coefficient | G = | 0.715 474
|
| Balanced inequality ratio | P = | 0.217 956
|
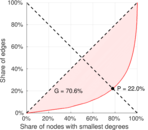
| Outdegree balanced inequality ratio | P+ = | 0.220 190
|
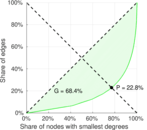
| Indegree balanced inequality ratio | P− = | 0.227 748
|
| Relative edge distribution entropy | Her = | 0.856 811
|
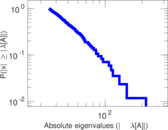
| Power law exponent | γ = | 1.968 88
|
| Tail power law exponent | γt = | 2.051 00
|
| Tail power law exponent with p | γ3 = | 2.051 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 2.061 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 2.271 00
|
| Indegree p-value | pi = | 0.002 000 00
|
| Degree assortativity | ρ = | −0.164 834
|
| Degree assortativity p-value | pρ = | 1.857 77 × 10−259
|
| In/outdegree correlation | ρ± = | +0.890 664
|
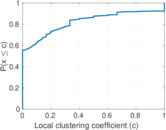
| Clustering coefficient | c = | 0.059 238 4
|
| Directed clustering coefficient | c± = | 0.055 367 2
|
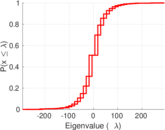
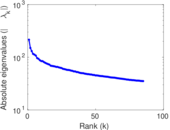
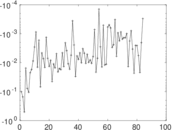
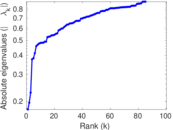
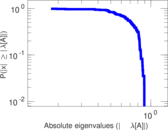
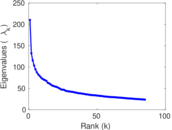
| Spectral norm | α = | 292.694
|
| Operator 2-norm | ν = | 205.822
|
| Cyclic eigenvalue | π = | 118.316
|
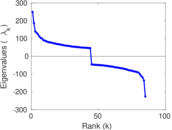
| Algebraic connectivity | a = | 0.253 255
|
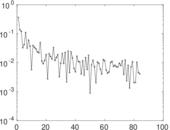
| Spectral separation | |λ1[A] / λ2[A]| = | 1.180 45
|
| Reciprocity | y = | 0.792 313
|
| Non-bipartivity | bA = | 0.481 386
|
| Normalized non-bipartivity | bN = | 0.039 855 0
|
| Algebraic non-bipartivity | χ = | 0.072 874 3
|
| Spectral bipartite frustration | bK = | 0.002 490 44
|
| Negativity | ζ = | 0.100 107
|
| Algebraic conflict | ξ = | 0.140 294
|
| Triadic conflict | τ = | 0.127 519
|
| Spectral signed frustration | φ = | 0.004 875 71
|
| Controllability | C = | 3,120
|
| Relative controllability | Cr = | 0.530 522
|
Plots

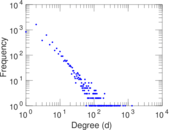
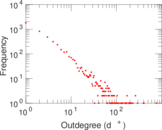
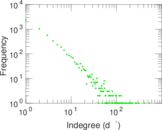
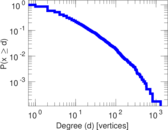
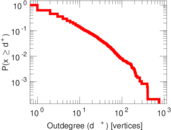
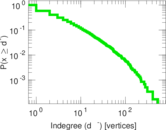
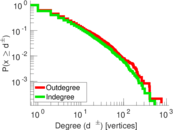
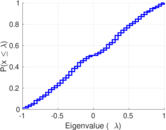
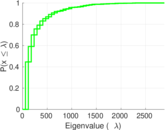
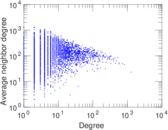
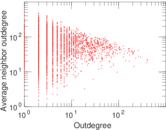
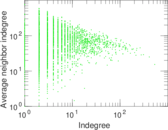
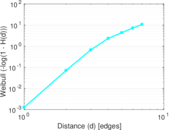
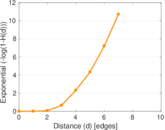



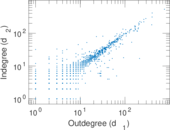
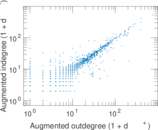
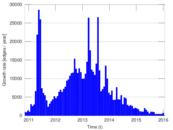
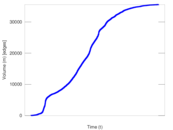
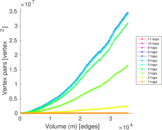
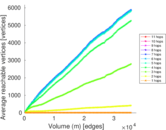
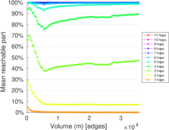
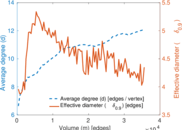
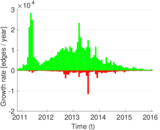
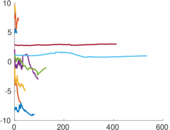

Matrix decompositions plots
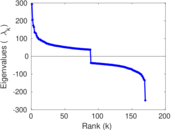
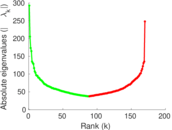
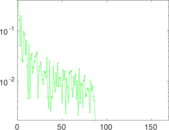
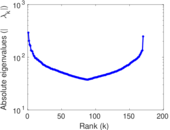
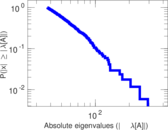
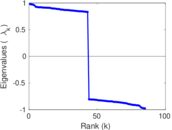
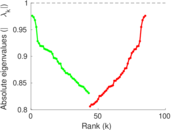
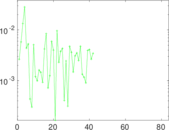
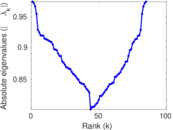
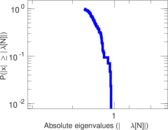
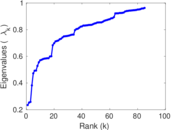
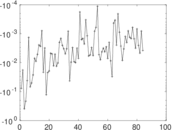
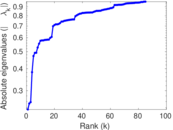
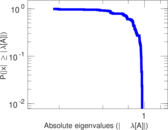
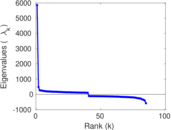
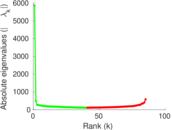
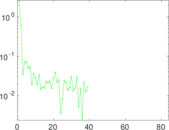
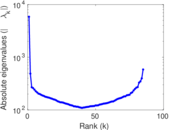
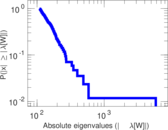
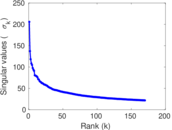
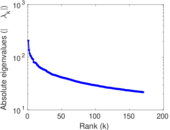
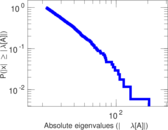
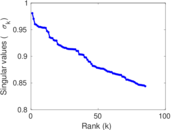
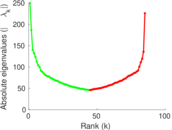
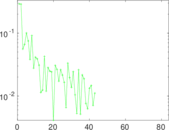
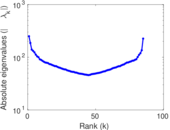
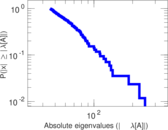
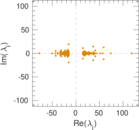
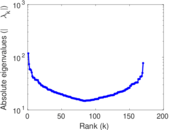
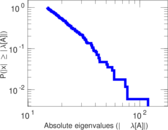
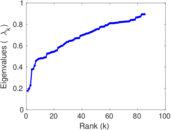
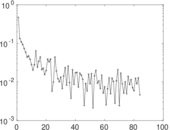
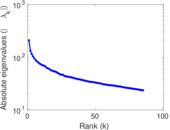
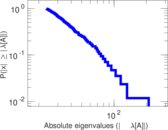
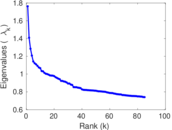
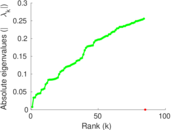
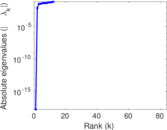
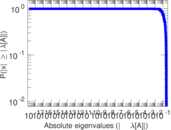
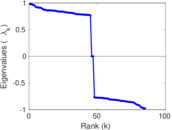
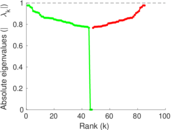
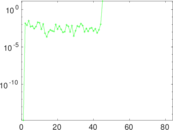
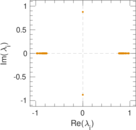
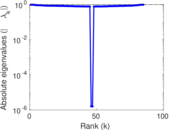
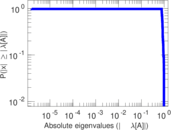
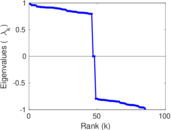
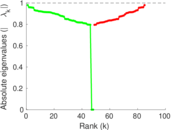
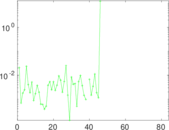
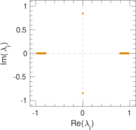
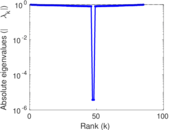
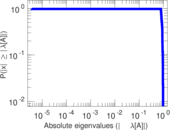
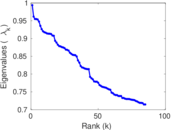
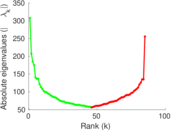
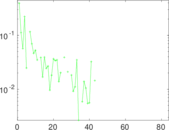
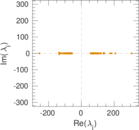
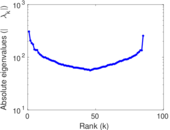
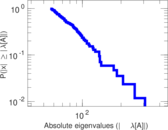
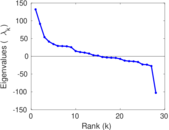
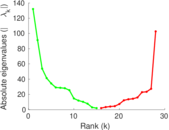
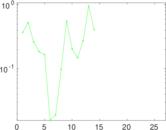
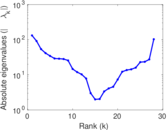
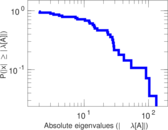
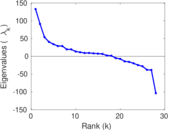
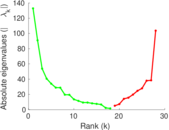
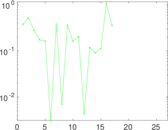
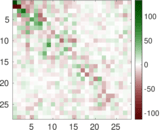
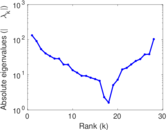
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Srijan Kumar, Francesca Spezzano, V. S. Subrahmanian, and Christos Faloutsos.
Edge weight prediction in weighted signed networks.
In Proc. Int. Conf. Data Min., pages 221–230, 2016.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee