TripAdvisor
This is the rating network from TripAdvisor, where users rate individual
hotels. We filtered out ratings for which the username was "lass=" (26,590
instances) and "A TripAdvisor Member" (37,704 instances), as these are probably
anonymous ratings, or errors in the dataset.
Metadata
Statistics
| Size | n = | 147,075
|
| Left size | n1 = | 145,316
|
| Right size | n2 = | 1,759
|
| Volume | m = | 175,765
|
| Unique edge count | m̿ = | 175,655
|
| Wedge count | s = | 23,704,235
|
| Claw count | z = | 5,893,488,792
|
| Cross count | x = | 2,022,222,569,935
|
| Square count | q = | 11,327
|
| 4-Tour count | T4 = | 95,259,242
|
| Maximum degree | dmax = | 2,138
|
| Maximum left degree | d1max = | 22
|
| Maximum right degree | d2max = | 2,138
|
| Average degree | d = | 2.390 14
|
| Average left degree | d1 = | 1.209 54
|
| Average right degree | d2 = | 99.923 3
|
| Fill | p = | 0.000 687 197
|
| Average edge multiplicity | m̃ = | 1.000 63
|
| Size of LCC | N = | 146,988
|
| Diameter | δ = | 14
|
| 50-Percentile effective diameter | δ0.5 = | 5.478 03
|
| 90-Percentile effective diameter | δ0.9 = | 7.153 99
|
| Median distance | δM = | 6
|
| Mean distance | δm = | 5.949 55
|
| Gini coefficient | G = | 0.572 841
|
| Balanced inequality ratio | P = | 0.291 614
|
| Left balanced inequality ratio | P1 = | 0.450 867
|
| Right balanced inequality ratio | P2 = | 0.317 480
|
| Relative edge distribution entropy | Her = | 0.848 532
|
| Power law exponent | γ = | 6.925 22
|
| Tail power law exponent | γt = | 2.981 00
|
| Tail power law exponent with p | γ3 = | 2.981 00
|
| p-value | p = | 0.000 00
|
| Left tail power law exponent with p | γ3,1 = | 3.311 00
|
| Left p-value | p1 = | 0.000 00
|
| Right tail power law exponent with p | γ3,2 = | 2.231 00
|
| Right p-value | p2 = | 0.000 00
|
| Degree assortativity | ρ = | −0.099 365 7
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| Spectral norm | α = | 28.736 5
|
| Algebraic connectivity | a = | 0.000 126 145
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.020 81
|
| Negativity | ζ = | 0.409 877
|
| Algebraic conflict | ξ = | 0.004 594 92
|
| Spectral signed frustration | φ = | 0.000 480 856
|
| Controllability | C = | 143,557
|
| Relative controllability | Cr = | 0.976 080
|
Plots

















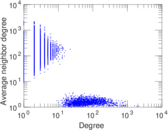




























Matrix decompositions plots





















Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Hongning Wang, Yue Lu, and Chengxiang Zhai.
Latent aspect rating analysis on review text data: A rating
regression approach.
In Proc. Int. Conf. on Knowl. Discov. and Data Min., pages
783–792, 2010.
|
|
[3]
|
Hongning Wang, Yue Lu, and ChengXiang Zhai.
Latent aspect rating analysis without aspect keyword supervision.
In Proc. Int. Conf. on Knowl. Discov. and Data Min., pages
618–626, 2011.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee




































































