Chess
These are results of chess games. Each node is a chess player, and a directed
edge represents a game, with the white player having an outgoing edge and the
black player having an ingoing edge. The weight of the edge represents the
outcome (+1 white won, 0 draw, −1 black won). The dataset is anonymous: the
identity of the players is unknown, and timestamps are approximate. Timestamps
are given to a one month precision, and may have been shifted towards the
future by an unknown amount.
Metadata
Statistics
| Size | n = | 7,301
|
| Volume | m = | 65,053
|
| Unique edge count | m̿ = | 34,564
|
| Loop count | l = | 0
|
| Wedge count | s = | 2,588,788
|
| Claw count | z = | 16,498,559
|
| Cross count | x = | 272,731,448
|
| Triangle count | t = | 108,595
|
| Square count | q = | 324,301
|
| 4-Tour count | T4 = | 6,216,178
|
| Maximum degree | dmax = | 280
|
| Maximum outdegree | d+max = | 152
|
| Maximum indegree | d−max = | 140
|
| Average degree | d = | 17.820 3
|
| Fill | p = | 0.000 741 048
|
| Average edge multiplicity | m̃ = | 1.882 10
|
| Size of LCC | N = | 7,115
|
| Size of LSCC | Ns = | 4,738
|
| Relative size of LSCC | Nrs = | 0.648 952
|
| Diameter | δ = | 13
|
| 50-Percentile effective diameter | δ0.5 = | 3.392 21
|
| 90-Percentile effective diameter | δ0.9 = | 4.831 00
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 3.949 93
|
| Gini coefficient | G = | 0.590 957
|
| Balanced inequality ratio | P = | 0.270 918
|
| Outdegree balanced inequality ratio | P+ = | 0.287 091
|
| Indegree balanced inequality ratio | P− = | 0.293 311
|
| Relative edge distribution entropy | Her = | 0.928 663
|
| Power law exponent | γ = | 1.617 64
|
| Tail power law exponent | γt = | 3.071 00
|
| Tail power law exponent with p | γ3 = | 3.071 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 3.061 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 3.061 00
|
| Indegree p-value | pi = | 0.000 00
|
| Degree assortativity | ρ = | +0.306 204
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.805 364
|
| Clustering coefficient | c = | 0.125 845
|
| Directed clustering coefficient | c± = | 0.040 989 8
|
| Spectral norm | α = | 18.856 4
|
| Operator 2-norm | ν = | 13.746 3
|
| Cyclic eigenvalue | π = | 3.192 15
|
| Algebraic connectivity | a = | 0.085 875 0
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.138 15
|
| Reciprocity | y = | 0.071 345 9
|
| Non-bipartivity | bA = | 0.652 749
|
| Normalized non-bipartivity | bN = | 0.051 195 9
|
| Algebraic non-bipartivity | χ = | 0.086 281 2
|
| Spectral bipartite frustration | bK = | 0.002 148 26
|
| Negativity | ζ = | 0.419 222
|
| Algebraic conflict | ξ = | 0.076 742 9
|
| Triadic conflict | τ = | 0.493 546
|
| Spectral signed frustration | φ = | 0.001 957 64
|
| Controllability | C = | 1,465
|
| Relative controllability | Cr = | 0.214 495
|
Plots

















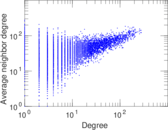

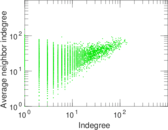


















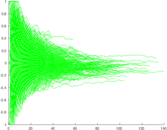
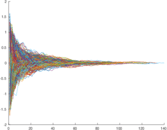
















Matrix decompositions plots













































































































Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee




































































































































































